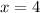А) соответственные углы при пересечении двух парал. прямых третьей равны, значит 2х=240°; х=240°/2; х=120°. у=180°-120°=60°. ответ: 120° и 60°.
Б) внутренние односторонние углы при параллельных в сумме дают 180°. Если меньший из них принять за х, то второй х+20°, а их сумма х+х+20°=180°; 2х+20°=180°; 2х=180°-20°; 2х=160° х=160°/2 х=80° 80°+20°=100° ответ: 80° и 100°.
В) Накрест лежащие углы при параллельных равны, поэтому можно их (каждый из них принять за х. Тогда 2х=250° х=250°/2 х=125° 180°-125°=55° ответ: 125° и 55°.
В иррациональных уравнениях кроме ОДЗ нужно всегда учитывать дополнительные условия (ДУ) или всегда для проверки подставлять полученные корни в исходное уравнение.
Рассмотрим исходное уравнение:
Далее мы возводим это уравнение в квадрат, но это неэквивалентный переход - например, неправильное равенство -1 = 1 переходит в правильное 1 = 1, поэтому на этом этапе легко приобрести лишние корни, что и произошло.
В правой части исходного уравнения находится неотрицательный корень, поэтому в ДУ необходимо потребовать неотрицательность левой части:
Как раз это ДУ и позволяет в процессе решения откинуть лишний корень
2х=240°;
х=240°/2;
х=120°.
у=180°-120°=60°.
ответ: 120° и 60°.
Б) внутренние односторонние углы при параллельных в сумме дают 180°. Если меньший из них принять за х, то второй х+20°, а их сумма
х+х+20°=180°;
2х+20°=180°;
2х=180°-20°;
2х=160°
х=160°/2
х=80°
80°+20°=100°
ответ: 80° и 100°.
В) Накрест лежащие углы при параллельных равны, поэтому можно их (каждый из них принять за х. Тогда
2х=250°
х=250°/2
х=125°
180°-125°=55°
ответ: 125° и 55°.
В иррациональных уравнениях кроме ОДЗ нужно всегда учитывать дополнительные условия (ДУ) или всегда для проверки подставлять полученные корни в исходное уравнение.
Рассмотрим исходное уравнение: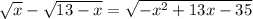
Далее мы возводим это уравнение в квадрат, но это неэквивалентный переход - например, неправильное равенство -1 = 1 переходит в правильное 1 = 1, поэтому на этом этапе легко приобрести лишние корни, что и произошло.
В правой части исходного уравнения находится неотрицательный корень, поэтому в ДУ необходимо потребовать неотрицательность левой части: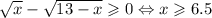
Как раз это ДУ и позволяет в процессе решения откинуть лишний корень