Алгебра: Постройте параболы по условиям

Постройте параболы по условиям

Показать ответ

Ответ:

милан64488

12.07.2022 04:52

4+16=20 кг общая масса кислоты
20*0.57=11.4 кг активного в-ва в растворе
пусть х концентрация кислоты в первом сосуде ,
тогда 4*х масса активного в-ва в первом сосуде
пусть у концентрация кислоты во втором сосуде
тогда 16у масса активного в-ва во втором сосуде
получим 4х+16у=11.4
составим второе уравнение возьмем одинаковое количество из двух сосудов по 4 кг ,получим 4х+4у=8*0.6 (кг активного в-ва )
4х+4у=4.8
выразим значение у у=(4.8-4х) /4
у=1,2-х , подставим в первое ур-е
4х+16(1,2-х)=11.4
4х+19,2-16х=11,4
-12х=11,4-19.2
-12х=-7.8
х=0,65
ответ : концентрация р-ра в первом сосуде 65%

0,0(0 оценок)

Ответ:

АлинаRiver

29.07.2021 03:15

Объяснение:

Конечно же обе формулы дают ОДНИ И ТЕ ЖЕ решения. Просто запись в частном случае более лёгкая для восприятия.

$sinx=1\; \; \Rightarrow \; \; x=\frac{\pi}{2}+2\pi k\; ,\; k\in Z$

Из этой формулы следует, что sinx=1 при х=П/2 , причём, если эту точку повернуть на один круг (+/-2П), два круга (+/-4П), три круга (+/-6П) и так далее, то придём в одну ту же точку В на тригонометрическом круге с декартовыми координатами (0,1) . Смотри рисунок. Поворачивать точку можно против часовой стрелки (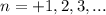 n=+1,2,3,... ) или по часовой стрелкe ( n=-1,-2,-3,... ) .

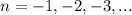В случае общей формулы надо рассматривать чётные и нечётные значения .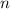

Если k- чётно, то получаем

$k=2n\, :\; \; x=(-1)^{2n}\cdot arcsin1+\pi \cdot 2n=+1\cdot \frac{\pi}2}+2\pi n,\; n\in Z$

То есть получили ту же формулу, что и в частном случае.

Если k - нечётно, то получаем

$k=2n-1\, :\; \; x=(-1)^{2n-1}\cdot arcsin1+\pi \cdot (2n-1)=-1\cdot \frac{\pi}{2}+\pi \cdot (2n-1)=\\\\=-\frac{\pi}{2}+2\pi n-\pi =-\frac{3\pi }{2}+2\pi n \; ,\; n\in Z$

На вид эта формула не похожа на частный случай, но точка х= -3П/2 получается из точки с дек. координатами А(1,0) путём её поворота на 270° (3П/2) по часовой стрелке (отрицательное направление поворота, поэтому знак (-) пишем ). И попадёт она в точку В(0,1). Но ведь мы попадём в точку В(0,1) и при повороте точки А(1,0) против часовой стрелки ( положительное направление поворота) на 90° (П/2) .

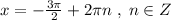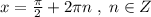Поэтому запись $x=-\frac{3\pi}{2}+2\pi n\; ,\; n\in Z$ равноценна записи $x=\frac{\pi}{2}+2\pi n\; ,\; n\in Z$ .

Конечно, предпочтительнее сразу писать частный вид формулы для решения уравнения sinx=1, потому что он более простой в записи , но описывает те же решения, что и частный случай.

0,0(0 оценок)

Популярные вопросы: Алгебра