Повна поверхня прямок тного паралелептеда , основою якого е квадрат , дорвное 264 см2 . знайдть сторону основи паралелет педа , якщо його висота дорвное 8 см .

Раскладываем вторую скобку по формуле разности кубов

Заметим, что неполный квадрат в третьей скобке всегда положителен

Докажем это

Так как квадраты не могут быть отрицательными.

Значит можно рассмотреть неравенство методом интервалов.

1) При х<0 первый множитель будет меньше нуля, второй тоже меньше нуля. Два множителя меньше нуля дадут положительное число. А третий будет положительным. Значит все выражение в левой части будет положительным.

2) При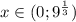 Первый множитель будет больше нуля, второй меньше нуля, а третий как всегда положителен. Отрицательный множитель помноженный на положительные множители даст в итоге отрицательное число.

3)

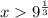
Первый множитель будет положителен, второй тоже положителен. А третий как всегда положителен. Значит в итоге, перемножив три положительных числа, получим положительное число.

В ответе получим два промежутка из первого и третьего случаев.

Заметно, что целочисленных решений будет бесконечно много. Это и все отрицательные целые числа и целые числа большие 2. Так как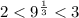

Решений, так сказать, счетное множество.

Ну, а если бы был бы в неравенстве противоположный знак, то было бы всего два решения из второго случая. Это числа 1 и 2.

1) x^2+3.5x-2=0

2x^2+7-4=0

D=49+32=81=9^2

X=-4;0.5

ответ: -4; 0.5

2) x^2-6x+24-4x+1=0

x^2-10x+25=0

D=100-100=0

x=3

ответ: 3

3) 2x^2-7x+9

D=49-72

Пустое множество

4) 7+2(x-4)                                         x+4

2x=1                                                    x=-4

x=0.5                          >                      x=-4

от - бесконечности до 0.5 и от 4 до плюс бесконечности все включительно

5) -0.4x+0.6                                      6x+1.5

x=-1.5                         <                      x=-0.25

от -1.5 до 0.25 все не включительно

6) -3x-6+2x-2                                    3x-9+2

-x=8                                                    3x=7

x=8                              >                    x=3.5

от - бесконечности до 3.5 и от 8 до плюс бесконечности все не включительно

д) x+1+2x+2+3x-3                            4x+3x-6

6x=0                                                    7x=6

x=0                               <                     x=6/7

от 0 до 6/7 все не включительно

г) x-1/3+7x-7                                      4x+2

-6x=22/3                                              x=-0.5

6x=-22/3                     <                        x=-0.5

от (-22/3)/6 до -0.5 все включительно