ПРЕОБРАЗОВАНИЕ ЦЕЛОГО ВЫРАЖЕНИЯ В МНОГОЧЛЕН
a)5x(x-y)-2(y-x)^2
б)(y+7)^2-2(y+10)(y+4)
в)(x-5)(6+4x)-3(1+x)^2

Решение
Пусть скорость первого велосипедиста - x км/ч.
Тогда скорость второго - (x+3) км/ч.
 Первый велосипедист проехал всё расстояние равное 
36 км за (36/x) часов.
Второй проехал это расстояние за (36/(x+3)) часов.
Известно, что второй велосипедист проехал расстояние
на 1 час быстрее. 
Составим уравнение: 
 36/x - 36/(x + 3) = 1 
36(x + 3) - 36x = x(x + 3)
36x + 108 - 36x = x² + 3x 
x² + 3x - 108 = 0
D = 9 + 4*108 = 441
 x₁ = (- 3 + 21)/2 = 9
x₂ = (- 3 - 21)/2  =- 12 < 0 не удовлетворяет условию задачи
9 км/ч - скорость первого велосипедиста
1) 9 + 3 = 12 (км/ч) - скорость второго велосипедиста
 ответ:  9 км/ч; 12 км/ч.

Пусть первоначальная масса сплава равна  М.  Тогда содержание меди в сплаве было    .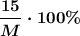

К сплаву добавили  20 кг меди, масса сплава стала    М+20 кг. Тогда содержание меди в сплаве стало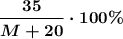    .    При этом содержание меди увеличилось на 20%.

(15 + 0,2M)(M + 20) = 35 M

15M + 0,2M² + 300 + 4M - 35M = 0

0,2M² - 16M + 300 = 0             |  × 5

M² - 80M + 1500 = 0

(M - 50)(M - 30) = 0

1)  M - 50 = 0;    M = 50    > 40    -   не подходит под условие

2)  M - 30 = 0;    M = 30 кг

ответ :  30 кг

=================================

Проверка :

  -  первоначальное содержание меди в сплаве.

 - содержание меди после добавления 20 кг.

70% - 50% = 20%