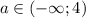Так как x = 0 не является корнем уравнения, поделим обе части на x.
Обозначим правую часть как f(x). Найдём производную этой функции:
Заметим, что при x = 1 числитель равен нулю. Разложим его на множители: . Второй множитель разложить нельзя, так как, приравняв его к нулю, мы не сможем найти корни, ибо D < 0. Найдём знаки производной (см. фото 1). Зная это, можем прикинуть график функции (см. фото 2). Точка локального минимума - x = 1. f(1) = 4.
a = k (k - какое-то число) - прямая, параллельная оси Ox. По графику видно, что при a < 4 имеется ровно одно пересечение, то есть один корень.
Пусть х (дней) печатала одна типография, тогда вторая печатала
(х - 2) дня.
15 000х экземпляров - напечатала одна типография
10 000 (х - 2) экземпляров - напечатала вторая
Всего 250 000 экземпляров.
Составим уравнение:
15 000х + 10 000 * (х - 2) = 250 000
15 000х + 10 000х - 20 000 = 250 000
25 000х = 270 000
х = 270 000 : 25 000
х = 10,8 (дней) - округляем до целого ≈ 11 дней
ответ: весь тираж был напечатан за 11 дней.
По действиям:
1) 15 000 * 2 = 30 000 экз. - напечатала одна типография (пока вторая простаивала)
2) 250 000 - 30 000 = 220 000 экз. - печатали вместе
3) 15 000 + 10 000 = 25 000 экз./день - общая производительность
4) 220 000 : 25 000 = 8,8 дня
5) 8,8 + 2 = 10,8 ≈ 11 дней
ответ: тираж напечатали за 11 дней.
Так как x = 0 не является корнем уравнения, поделим обе части на x.
Обозначим правую часть как f(x). Найдём производную этой функции:
Заметим, что при x = 1 числитель равен нулю. Разложим его на множители: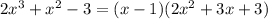 . Второй множитель разложить нельзя, так как, приравняв его к нулю, мы не сможем найти корни, ибо D < 0. Найдём знаки производной (см. фото 1). Зная это, можем прикинуть график функции (см. фото 2). Точка локального минимума - x = 1. f(1) = 4.
. Второй множитель разложить нельзя, так как, приравняв его к нулю, мы не сможем найти корни, ибо D < 0. Найдём знаки производной (см. фото 1). Зная это, можем прикинуть график функции (см. фото 2). Точка локального минимума - x = 1. f(1) = 4.
a = k (k - какое-то число) - прямая, параллельная оси Ox. По графику видно, что при a < 4 имеется ровно одно пересечение, то есть один корень.
ответ: