«Просчитав» несколько первых переливаний, нетрудно обнаружить, что после первого, третьего, пятого переливаний в обоих сосудах будет по ½ л воды. Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k + 1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды.
Т.к. это система неравенства мы эти оба графика соединяем в один и смотрим пересечение.
У нас сначала получился сектор, но т.к. сказано найти фигуру, то мы проводим хорду, которая будет являться гипотенузой равнобедренного(он равнобедренный из-за того, что его катеты это радиус окружности) прямоугольного треугольника. Этот равнобедренный прямоугольник треугольник входит в сектор, который является промежутком этой системы неравенства.
ответ получается 2 см^2
Объяснение:
Мы должны понять, что это за графики
(1) Это график с модулем
(2) Это график окружности
Т.к. это система неравенства мы эти оба графика соединяем в один и смотрим пересечение.
У нас сначала получился сектор, но т.к. сказано найти фигуру, то мы проводим хорду, которая будет являться гипотенузой равнобедренного(он равнобедренный из-за того, что его катеты это радиус окружности) прямоугольного треугольника. Этот равнобедренный прямоугольник треугольник входит в сектор, который является промежутком этой системы неравенства.
По формуле окружности можно понять что R=2 см
Площадь тогда будет S=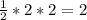 см^2
см^2