Преобразуйте в многочлен: а) (х-5)(х+5) б) (n+4)^2 в) (x-5)(х+5) г) (4x-y)(y+4x) У выражение: (2-с)^2-с(с+4) и найдите его значение при с=0,5 Разложите на множители: а) 4а^2-6аb б) 9x^2-44, в) 25-b^2, г) у^2-4у+у Решите уравнение: 21-2(3-4х)=3-2х
Введем функции и . Про вторую сразу скажем, что , но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это при или . Тогда наименьшее значение этой функции будет равно .
Теперь разберемся с . У нас есть квадратный корень, поэтому все значения функции точно . Но и здесь мы идем дальше. Поменяем временно на букву . Тогда будет . Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное при , откуда .
Наибольшее значение равно и достигается при . Наименьшее значение равно и достигается при или .
по свойству квадратичной функции выражение 3x²+6x+7
имеет минимальное значение в вершине параболы
по формуле координат вершины параболы
х₀=-b/(2a)=-6/(2*3)=-1
y₀=y(х₀)=3(-1)²+6(-1)+7=3-6+7=4
2) рассмотрим квадратичную функцию y=5x²+10x+14
аналогично рассуждая делаем вывод, что выражение 5x²+10x+14
имеет минимальное значение в вершине параболы
по формуле координат вершины параболы
х₀=-b/(2a)=-10/(2*5)=-1
y₀=y(х₀)=5(-1)²+10(-1)+14=5-10+14=9
3) рассмотрим квадратичную функцию y=-x²-2х+4
так как коэффициент при x² равен -1 и -1<0 то
по свойству квадратичной функции выражение -x²-2х+4
имеет максимальное значение в вершине параболы
по формуле координат вершины параболы
х₀=-b/(2a)=2/(2*(-1))=-1
y₀=y(х₀)=-(-1)²-2(-1)+4=-1+2+4=5
4) соответственно
выражение
√(3x²+6x+7) + √(5x²+10x+14) имеет минимум при х=-1 и его минимальное значение равно √4+√9=2+3=5
так как левая часть исходного уравнения имеет минимум в точке x=-1
а правая часть имеет максимум в этой же точке и значения в этой точке левой и правой части уравнения совпадают то в этой точке уравнение имеет корень х=-1 и он единственный
(см. объяснение)
Объяснение:
Введем функции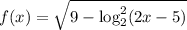 и
и 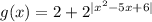 . Про вторую сразу скажем, что
. Про вторую сразу скажем, что 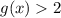 , но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это
, но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это 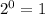 при
при 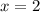 или
или 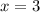 . Тогда наименьшее значение этой функции будет равно
. Тогда наименьшее значение этой функции будет равно 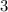 .
.
Теперь разберемся с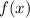 . У нас есть квадратный корень, поэтому все значения функции точно
. У нас есть квадратный корень, поэтому все значения функции точно 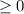 . Но и здесь мы идем дальше. Поменяем временно
. Но и здесь мы идем дальше. Поменяем временно 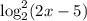 на букву
на букву 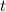 . Тогда будет
. Тогда будет 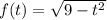 . Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное
. Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное 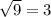 при
при 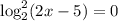 , откуда
, откуда 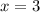 .
.
Наибольшее значение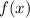 равно
равно 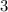 и достигается при
и достигается при 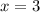 . Наименьшее значение
. Наименьшее значение 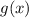 равно
равно 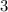 и достигается при
и достигается при 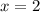 или
или 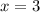 .
.
Тогда единственный корень исходного уравнения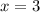 .
.
Уравнение решено!
Уравнение имеет один корень
Объяснение:
1) рассмотрим квадратичную функцию y=3x²+6x+7
так как коэффициент при x² равен 3 и 3>0 то
по свойству квадратичной функции выражение 3x²+6x+7
имеет минимальное значение в вершине параболы
по формуле координат вершины параболы
х₀=-b/(2a)=-6/(2*3)=-1
y₀=y(х₀)=3(-1)²+6(-1)+7=3-6+7=4
2) рассмотрим квадратичную функцию y=5x²+10x+14
аналогично рассуждая делаем вывод, что выражение 5x²+10x+14
имеет минимальное значение в вершине параболы
по формуле координат вершины параболы
х₀=-b/(2a)=-10/(2*5)=-1
y₀=y(х₀)=5(-1)²+10(-1)+14=5-10+14=9
3) рассмотрим квадратичную функцию y=-x²-2х+4
так как коэффициент при x² равен -1 и -1<0 то
по свойству квадратичной функции выражение -x²-2х+4
имеет максимальное значение в вершине параболы
по формуле координат вершины параболы
х₀=-b/(2a)=2/(2*(-1))=-1
y₀=y(х₀)=-(-1)²-2(-1)+4=-1+2+4=5
4) соответственно
выражение
√(3x²+6x+7) + √(5x²+10x+14) имеет минимум при х=-1 и его минимальное значение равно √4+√9=2+3=5
так как левая часть исходного уравнения имеет минимум в точке x=-1
а правая часть имеет максимум в этой же точке и значения в этой точке левой и правой части уравнения совпадают то в этой точке уравнение имеет корень х=-1 и он единственный