Преобразуйте в многочлен стандартного вида:
а) (x2+5x)2
б) (0,5у-3)2
в) (х-5)(х+5)
г) (4а-b)(4a+b)

task/30647175  Решить уравнение √(3x²- 4x+15) +√(3x²- 4x+8) = 7

решение    ОДЗ :  x ∈ ( - ∞ ; ∞ ) ,  т.к.

3x²- 4x+8=3(x -2/3)²+20/3 ≥ 20/3   >  0   || D₁=2² -3*8 = -24 < 0 || следовательно  и 3x²- 4x+15 = ( 3x²- 4x+8 ) + 7  > 0                                           * * * 3(x -2/3)² +41/3  ≥  41/3 * * *

замена : t = 3x²- 4x+ 8 ≥ 20/3 ; √(t +7) + √t =7 ⇔√( t +7 ) = 7 - √t  

возведем обе части уравнения √( t +7 ) = 7 - √t  в квадрат

* * * необходимо  7 - √t  ≥ 0  ⇔ √t ≤ 7 ⇔  0 ≤ t ≤ 49    * * *

t +7 = 49 -14√t + t ⇔ 14√t  = 42  ⇔ √t  =3 ⇔  t  = 9   || 7 - √t = 4 >0 ||

3x²- 4x+8 = 9 ⇔ 3x²- 4x -1 =0 ;  D₁ = 2² -3*(-1) =7= (√7)²    

x₁  =(2 -√7) / 3   ; x₂ = (2+√7)/3 .

ответ :   (2 ±√7)/3  .

Формула работы: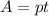    , р - производительность , t- время .

Если 6 насосов выкачивают воду из 1 бассейна за 10 часов, то за 1 час эти 6 насосов выкачают 1/10 часть бассейна. То есть производительность  6-ти насосов = 1/10 бассейна в час.

Производительность же 1 насоса равна (1/10):6=1/60  бассейна в час.

а) За 5 часов всю воду из 1 бассейна выкачают n насосов, то есть можно записать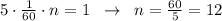    насосов.

За 15 часов  всю воду из 1 бассейна выкачивают m насосов, то есть можно записать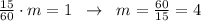    насоса.

б)  Три насоса за 1 час выкачивают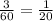    часть бассейна, значит всю воду из 1 бассейна три насоса выкачают за  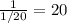  часов.

9 насосов за 1 час выкачивают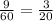    часть бассейна, значит всю воду из 1 бассейна 9 насосов выкачают за  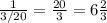  часa.