Задание 1
Попробуем каждую из пар чисел. Какая даст верное тождество, та и есть решение.
а)
Этот вариант не подходит. Проверяем дальше.
б)
Этот вариант подходит. Проверяем дальше.
в)
Этот вариант не подходит. Проверяем последнюю пару чисел.
г)
Этот вариант подходит.
ответ к Заданию 1: Решениями уравнения являются пары чисел и .
Задание 2
Пара чисел является решением уравнения . Нужно найти . Второе число это координата . Это означает, что .
ответ к Заданию 2:
Задание 3
При каком значении пара чисел будет являть решением уравнения?
ответ к Заданию 3: ;
Задание 4
Точка А принадлежит графику .
Точка B не принадлежит графику
Точка C принадлежит графику .
ответ к Заданию 4: точки А и С принадлежат графику , а точка В не принадлежит этому графику.
300 : 2 = 150 км - половина пути
30 мин = 0,5 ч
Пусть х км/ч - скорость поезда до остановки, тогда (х + 10) км/ч - скорость поезда после остановки. Уравнение:
150/х - 150/(х+10) = 0,5
150 · (х + 10) - 150 · х = 0,5 · х · (х + 10)
150х + 1500 - 150х = 0,5х² + 5х
0,5х² + 5х - 1500 = 0
D = b² - 4ac = 5² - 4 · 0,5 · (-1500) = 25 + 3000 = 3025
√D = √3025 = 55
х₁ = (-5-55)/(2·0,5) = (-60)/1 = -60
х₂ = (-5+55)/(2·0,5) = 50/1 = 50
ответ: 50 км/ч.
Проверка:
150/50 - 150/(50+10) = 150/50 - 150/60 = 3 - 2,5 = 0,5 ч = 30 мин
Задание 1
Попробуем каждую из пар чисел. Какая даст верное тождество, та и есть решение.
а)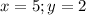
Этот вариант не подходит. Проверяем дальше.
б)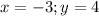
Этот вариант подходит. Проверяем дальше.
в)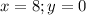
Этот вариант не подходит. Проверяем последнюю пару чисел.
г)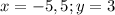
Этот вариант подходит.
ответ к Заданию 1: Решениями уравнения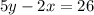
являются пары чисел 
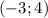и 
.
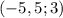Задание 2
Пара чисел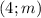
является решением уравнения . Нужно найти . Второе число это координата 
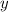. Это означает, что 
.
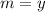ответ к Заданию 2: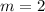
Задание 3
При каком значении
пара чисел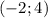 
будет являть решением уравнения?
ответ к Заданию 3: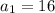
; 
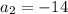
Задание 4
Точка А принадлежит графику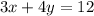
.
Точка B не принадлежит графику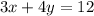
Точка C принадлежит графику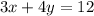
.
ответ к Заданию 4: точки А и С принадлежат графику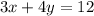
, а точка В не принадлежит этому графику.
300 : 2 = 150 км - половина пути
30 мин = 0,5 ч
Пусть х км/ч - скорость поезда до остановки, тогда (х + 10) км/ч - скорость поезда после остановки. Уравнение:
150/х - 150/(х+10) = 0,5
150 · (х + 10) - 150 · х = 0,5 · х · (х + 10)
150х + 1500 - 150х = 0,5х² + 5х
0,5х² + 5х - 1500 = 0
D = b² - 4ac = 5² - 4 · 0,5 · (-1500) = 25 + 3000 = 3025
√D = √3025 = 55
х₁ = (-5-55)/(2·0,5) = (-60)/1 = -60
х₂ = (-5+55)/(2·0,5) = 50/1 = 50
ответ: 50 км/ч.
Проверка:
150/50 - 150/(50+10) = 150/50 - 150/60 = 3 - 2,5 = 0,5 ч = 30 мин