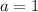При каких значениях а, система уравнений
а) имеет единственное решение
б) не имеет решений
в) имеет бесконечное множество решений​

Разделим обе части второго уравнения на 2:

Решим систему уравнений методом подстановки. Выразим переменную из второго уравнения:

Подставим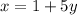 в первое уравнение системы:

Решим данное уравнение в зависимости от значений параметра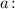

Если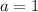 , то 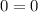, значит, 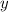— любое число.

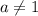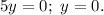Если , то Тогда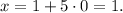

Система уравнений всегда имеет решения.

а)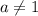

б)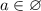

в)