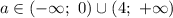Построим график функции y = 3x^2 - x^3 :
Уравнение будет иметь ровно 1 корень, если значения параметра а будет находить в синей области.
Найдем точки экстремумы функции y = 3x^2 - x^3 :
y' = 6x - 3x^2
6x-3x^2 = 0
3x(2-x) = 0
[ x = 0
[ x = 2
Подставим в функцию :
Значит a ∈ (-∞ ; 0) U (4 ; +∞)
ответ : При a ∈ (-∞ ; 0) U (4 ; +∞)
Рассмотрим две функции: и
Изобразим на координатной плоскости график функции
Функция не обладает свойством четности.
3) Находим абсциссы точек пересечения графика с осью
Находим ординату точки пересечения графика с осью
4) Находим производную:
Критические точки:
5) Составим таблицу (см. вложение).
7) Используя результаты исследования, построим схематический график функции (см. вложение).
Тогда уравнение будет иметь единственное решение, если графики функций и будут иметь единственное пересечение.
Так произойдет, если и
ответ:
Построим график функции y = 3x^2 - x^3 :
Уравнение будет иметь ровно 1 корень, если значения параметра а будет находить в синей области.
Найдем точки экстремумы функции y = 3x^2 - x^3 :
y' = 6x - 3x^2
6x-3x^2 = 0
3x(2-x) = 0
[ x = 0
[ x = 2
Подставим в функцию :
Значит a ∈ (-∞ ; 0) U (4 ; +∞)
ответ : При a ∈ (-∞ ; 0) U (4 ; +∞)
Рассмотрим две функции: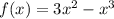 и
и 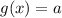
Изобразим на координатной плоскости график функции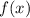
Функция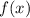 не обладает свойством четности.
не обладает свойством четности.
3) Находим абсциссы точек пересечения графика с осью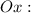
Находим ординату точки пересечения графика с осью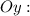
4) Находим производную:
Критические точки:
5) Составим таблицу (см. вложение).
7) Используя результаты исследования, построим схематический график функции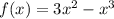 (см. вложение).
(см. вложение).
Тогда уравнение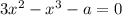 будет иметь единственное решение, если графики функций
будет иметь единственное решение, если графики функций 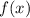 и
и 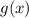 будут иметь единственное пересечение.
будут иметь единственное пересечение.
Так произойдет, если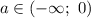 и
и 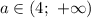
ответ: