Т.к. многочлен x³+ax²+bx+c делится нацело и на двучлен х-1 и на двучлен х+2, то он делится нацело и на произведение
(x-1)(x+2)=x²+x-2.
Т.к. степень многочлена x³+ax²+bx+c равна 3, а степень трехчлена x²+x-2 равна 2, то частное от их деления есть двучлен вида х-k.
Т.е. (x²+x-2)(x-k) = x³+ax²+bx+c. Раскроем скобки в левой части:
x³+x²-2x-kx²-kx+2k = x³+ax²+bx+c
x³+(1-k)x²+(-2-k)x+2k = x³+ax²+bx+c
Используя метод неопределенных коэффициентов, получим соотношения для a, b и с:
a = 1-k, b = -2-k, с = 2k.
Т.к. при делении x³+ax²+bx+c на х+1 в остатке получается 10, то по свойству делимости многочленов значение многочлена x³+ax²+bx+c при х = -1 должно быть равно 10, т.е. (-1)³+a(-1)²+b(-1)+c = 10, отсюда a-b+c=11.
2x−1
.
Для этого надо разложить числитель на множители.
Воспользуемся формулой ax 2+bx+c = a(x−x 1)(x−x 2)
где x 1 и x 2 — корни уравнения ax 2+bx+c = 0 .
Решим уравнение: 2x 2−3x+1 = 0 .
D = b 2 – 4ac = (–3) 2 – 4•2•1 = 9 – 8 = 1 ;
x 1 = −b+√ D
2a
; x 2 = −b−√ D
2a
.
x 1 = 3+√ 1
2•2
= 1 ; x 2 = 3−1
2•2
= 0,5.
Разложим квадратный трёхчлен в числителе на множители;
2x 2−3x+1
2x−1
= 2(x−1)(x−0,5)
2x−1
=
вынесем 2 в знаменателе за скобку.
= 2(x−1)(x−0,5)
2(x−0,5)
= x−1 ; при 2x – 1 ≠ 0 ⇒ x ≠ 0,5 .
Вывод: 2x 2−3x+1
2x−1
= x−1 при x ≠ 0,5 .
Т.к. многочлен x³+ax²+bx+c делится нацело и на двучлен х-1 и на двучлен х+2, то он делится нацело и на произведение
(x-1)(x+2)=x²+x-2.
Т.к. степень многочлена x³+ax²+bx+c равна 3, а степень трехчлена x²+x-2 равна 2, то частное от их деления есть двучлен вида х-k.
Т.е. (x²+x-2)(x-k) = x³+ax²+bx+c. Раскроем скобки в левой части:
x³+x²-2x-kx²-kx+2k = x³+ax²+bx+c
x³+(1-k)x²+(-2-k)x+2k = x³+ax²+bx+c
Используя метод неопределенных коэффициентов, получим соотношения для a, b и с:
a = 1-k, b = -2-k, с = 2k.
Т.к. при делении x³+ax²+bx+c на х+1 в остатке получается 10, то по свойству делимости многочленов значение многочлена x³+ax²+bx+c при х = -1 должно быть равно 10, т.е. (-1)³+a(-1)²+b(-1)+c = 10, отсюда a-b+c=11.
Решим систему уравнений: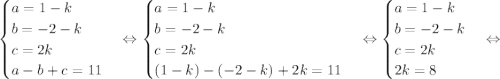
ответ: а = -3, b = -6, с = 8.