Объяснение:
Введем функцию:
Неопределенный интеграл:
- первообразная для функции
Найдем максимум функции :
следовательно функция имеет максимум
(при )
То есть максимум при
Условие:
При каком значении a значение интеграла максимально?
Ключевые слова:
Интегралы, определенный интеграл, интеграл с параметром, экстремумы функции, максимум функции
Объяснение:
Введем функцию: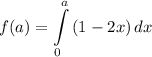
Неопределенный интеграл:
Найдем максимум функции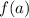 :
:
(при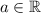 )
)
То есть максимум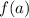 при
при 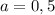
Условие:
При каком значении a значение интеграла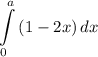 максимально?
максимально?
Ключевые слова:
Интегралы, определенный интеграл, интеграл с параметром, экстремумы функции, максимум функции