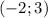Это уравнение окружности с центром в точке (0; 1) и радиусом √13.
Второе уравнение — прямая с коэффициентом . Он меньше 1, поэтому при некоторых значениях параметра прямая как бы пролетает сквозь дыру в первом графике, то есть система не имеет решений.
Система "начинает" иметь решения, когда прямая проходит через точки (3; 3) и выше или (-2; -2) и ниже. Нам нужно, чтобы прямая находилась между этими точками. Найдём граничные значения a:
Начертим график первого уравнения:
При![x^2-x-6\geq 0\Leftrightarrow x\in(-\infty;-2]\cup[3;+\infty)](/tpl/images/0454/4187/aa607.png) :
:
При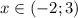 :
:
Это уравнение окружности с центром в точке (0; 1) и радиусом √13.
Второе уравнение — прямая с коэффициентом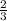 . Он меньше 1, поэтому при некоторых значениях параметра прямая как бы пролетает сквозь дыру в первом графике, то есть система не имеет решений.
. Он меньше 1, поэтому при некоторых значениях параметра прямая как бы пролетает сквозь дыру в первом графике, то есть система не имеет решений.
Система "начинает" иметь решения, когда прямая проходит через точки (3; 3) и выше или (-2; -2) и ниже. Нам нужно, чтобы прямая находилась между этими точками. Найдём граничные значения a:
ответ: