Квадратное уравнение не может иметь более двух решений. Однако, если в уравнении ax²+bx+c=0, где a,b,c=0, то уравнение превращается в 0x=0, тогда решений бесконечно много.
Если коэффициент при не равняется нулю, то тут более двух корней квадратное уравнение не будет иметь, так как согласно теореме алгебры квадратное уравнение имеет не более двух корней.
Осталось сделать все коэффициенты нулевыми
Общее а=2, т.е. при а = 2 уравнение превратится в 0х=0, где x - любой корень
Если коэффициент при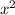 не равняется нулю, то тут более двух корней квадратное уравнение не будет иметь, так как согласно теореме алгебры квадратное уравнение имеет не более двух корней.
не равняется нулю, то тут более двух корней квадратное уравнение не будет иметь, так как согласно теореме алгебры квадратное уравнение имеет не более двух корней.
Осталось сделать все коэффициенты нулевыми
Общее а=2, т.е. при а = 2 уравнение превратится в 0х=0, где x - любой корень