Проверим : имеем уравнение - очевидно, не положительное решение, поэтому данное значение параметра не пойдет в ответ.
При уравнение - квадратное вида . Коэффициенты: (внезапно), , . Уравнение должно иметь корни по условию, т.е. его дискриминант как минимум не должен быть меньше 0.
Ищем дискриминант:
Найдем дискриминант трехчлена :
Это значит что при любых выражение , т.е. исходное уравнение всегда имеет 2 корня.
Могут быть три ситуации: 1) оба корня отрицательные; 2) корни имеют разные знаки; 3) оба корня положительные. Условию (нужно как минимум одно положительное решение) удовлетворяют только 2 и 3.
Проверим второй случай. Если корни имеют разные знаки, то достаточно условия . По теореме Виета Так как в нашем случае , то при любых . Т.е. при любых значениях параметра (кроме ) корни имеют разные знаки. Т.е. 3 случай уже можно не рассматривать, так как оба корня не могут быть положительными.
Проверим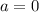 : имеем уравнение
: имеем уравнение 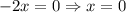 - очевидно, не положительное решение, поэтому данное значение параметра не пойдет в ответ.
- очевидно, не положительное решение, поэтому данное значение параметра не пойдет в ответ.
При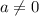 уравнение - квадратное вида
уравнение - квадратное вида 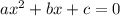 . Коэффициенты:
. Коэффициенты:  (внезапно),
(внезапно), 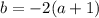 ,
,  . Уравнение должно иметь корни по условию, т.е. его дискриминант как минимум не должен быть меньше 0.
. Уравнение должно иметь корни по условию, т.е. его дискриминант как минимум не должен быть меньше 0.
Ищем дискриминант:
Найдем дискриминант трехчлена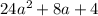 :
: 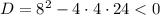
Это значит что при любых выражение
выражение 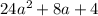
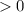 , т.е. исходное уравнение всегда имеет 2 корня.
, т.е. исходное уравнение всегда имеет 2 корня.
Могут быть три ситуации: 1) оба корня отрицательные; 2) корни имеют разные знаки; 3) оба корня положительные. Условию (нужно как минимум одно положительное решение) удовлетворяют только 2 и 3.
Проверим второй случай. Если корни имеют разные знаки, то достаточно условия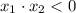 . По теореме Виета
. По теореме Виета 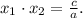 Так как в нашем случае
Так как в нашем случае 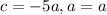 , то
, то 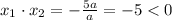 при любых
при любых  . Т.е. при любых значениях параметра (кроме
. Т.е. при любых значениях параметра (кроме 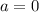 ) корни имеют разные знаки. Т.е. 3 случай уже можно не рассматривать, так как оба корня не могут быть положительными.
) корни имеют разные знаки. Т.е. 3 случай уже можно не рассматривать, так как оба корня не могут быть положительными.
Значит, нас устраивают любые , кроме
, кроме 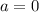 .
.
ОТВЕТ: при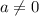 .
.