Среди всех троек , являющихся решением исходного уравнения выберем тройку такую, что сумма минимальна. Если существует более одной такой тройки, то выберем любую.
Рассмотрим уравнение по модулю 3: , что возможно только если делятся на 3. Пусть тогда . Имеем: , откуда ясно, что , откуда , поэтому . Подставим в уравнение: . То есть любому решению можно сопоставить решение , причем . Но для рассматриваемого решения сумма квадратов минимальна. Следовательно , что возможно только в случае, если , откуда следует .
Исследуем функцию на ее области определения: x є (1/e; +∞).
Слева имеем постоянную функцию, справа - монотонно возрастающую на области определения, поэтому уравнение имеет не более одного решения. Очевидно, что x = 1 - корень уравнения, а также - критическая точка функции
Вычислим знаки производной на интервалах (1/e; 1) и (1; +∞): возьмем, к примеру, числа 1/2 и e.
Имеем: , т.к. 1 - 2e < 0.
А из этого следует что числитель дроби положителен, что можно сказать и про знаменатель. Тогда f'(0,5)>0
Т.к. на интервале (1/e; 1) f'(x) > 0 , а на интервале (1; +∞) f'(x) < 0, x = 1 - точка максимума. Найдем значение максимума:\
Т.е. максимум равен f(1) = 0. Уже очевидно, что других корней уравнение иметь не будет, т.к. ни при каких других x максимум - 0 - достигаться не будет. А значит единственный корень уравнения - x = 1.
Среди всех троек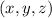
, являющихся решением исходного уравнения выберем тройку 
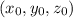такую, что сумма 
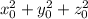минимальна. Если существует более одной такой тройки, то выберем любую.
Рассмотрим уравнение по модулю 3: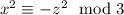
, что возможно только если 
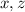делятся на 3. Пусть тогда 
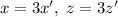. Имеем: 
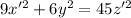, откуда ясно, что 
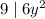, откуда 
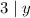, поэтому 
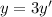. Подставим в уравнение: 
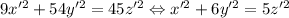. То есть любому решению 
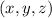можно сопоставить решение 
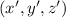, причем 
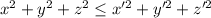. Но для рассматриваемого решения сумма квадратов минимальна. Следовательно 
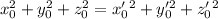, что возможно только в случае, если 
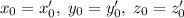, откуда следует 
.
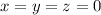Исследуем функцию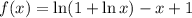
на ее области определения: x є (1/e; +∞).
Слева имеем постоянную функцию, справа - монотонно возрастающую на области определения, поэтому уравнение имеет не более одного решения. Очевидно, что x = 1 - корень уравнения, а также - критическая точка функции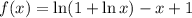
Вычислим знаки производной на интервалах (1/e; 1) и (1; +∞): возьмем, к примеру, числа 1/2 и e.
Имеем: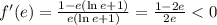
, т.к. 1 - 2e < 0.
А из этого следует что числитель дроби положителен, что можно сказать и про знаменатель. Тогда f'(0,5)>0
Т.к. на интервале (1/e; 1) f'(x) > 0 , а на интервале (1; +∞) f'(x) < 0, x = 1 - точка максимума. Найдем значение максимума:\
Т.е. максимум равен f(1) = 0. Уже очевидно, что других корней уравнение иметь не будет, т.к. ни при каких других x максимум - 0 - достигаться не будет. А значит единственный корень уравнения - x = 1.
ОТВЕТ: x = 1