Пусть - количество дней, за которое работу может выполнить первая бригада. У второй это займёт на 8 дней больше, то есть, . Работая вместе, они выполнили её за 3 дня. Составляем уравнение:
Приводим дроби к общему знаменателю :
Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. То есть:
Приравниваем числитель к нулю:
По теореме Виета:
-6 не подходит, поскольку количество дней не может быть отрицательным числом. Поэтому получаем, что первая бригада может выполнить работу за 4 дня.
Дано: Доказать, что — прямая пропорциональность. ---------- От нас требуется доказать, что — прямая пропорциональность, то есть доказать, что в выражении находится в первой степени (не , не , не и не , а просто ). Рассмотрим данное выражение . Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид , где , и . Формула «разность квадратов» раскрывается так: . Раскроем наше выражение по формуле: Упростим: . Итак, получается, что , находится в первой степени, а значит зависимость — есть прямая пропорциональность. Доказано.
Пусть - количество дней, за которое работу может выполнить первая бригада. У второй это займёт на 8 дней больше, то есть,
- количество дней, за которое работу может выполнить первая бригада. У второй это займёт на 8 дней больше, то есть, 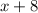 . Работая вместе, они выполнили её за 3 дня. Составляем уравнение:
. Работая вместе, они выполнили её за 3 дня. Составляем уравнение:
Приводим дроби к общему знаменателю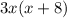 :
:
Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. То есть:
Приравниваем числитель к нулю:
По теореме Виета:
-6 не подходит, поскольку количество дней не может быть отрицательным числом. Поэтому получаем, что первая бригада может выполнить работу за 4 дня.
ответ: за 4 дня.
Доказать, что
----------
От нас требуется доказать, что
Рассмотрим данное выражение
Раскроем наше выражение по формуле:
Упростим:
Итак, получается, что