Пусть общий вид линейной системы уравнений , тогда эта система имеет бесконечно множество решений, если
В нашем случае система имеет бесконечно множество решений, когда
По теореме Виета
Из всех что подходит только a = 5.
ответ: при a = 5 система имеет бесконечно множество решений.
Пусть общий вид линейной системы уравнений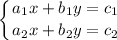 , тогда эта система имеет бесконечно множество решений, если
, тогда эта система имеет бесконечно множество решений, если 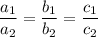
В нашем случае система имеет бесконечно множество решений, когда
По теореме Виета
Из всех что подходит только a = 5.
ответ: при a = 5 система имеет бесконечно множество решений.