7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1)
число в корне не может равняться отрицательному числу, корней уравнения нет.
2)
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1)
корней уравнения нет.
2)
корней уравнения нет.
=> уравнения равносильные.
9. 1)
ОДЗ: , ;
(не удовлетворяет ОДЗ),
ответ:
2)
,
ответ: ;
=> уравнения не равносильные.
10. 1)
ОДЗ: , ;
ответ:
2)
ответ:
=> уравнения равносильные.
12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
Для того,чтобы сумма квадратов корней уравнения равнялась какой-либо величине, эти корни должны существовать. Значит, дискриминант нашего уравнения должен быть неотрицательным,т.е (3p-5)^2-4(3p^2-11p-6)>=0. При таких "p" у исходного уравнения найдутся(возможно, совпадающие) корни x1 и x2. Запишем для них теорему Виета: x1+x2=-b/a=5-3p x1*x2=c/a=3p^2-11p-6 Теперь,не вычисляя корней, можно найти сумму их квадратов через "p": x1^2 + x2^2. Выделим полный квадрат: (x1+x2)^2-2x1*x2= (5-3p)^2-2(3p^2-11p-6). По условию, эта сумма квадратов равна 65. Получаем: (5-3p)^2-2(3p^2-11p-6)=65 Решим его: 25-30p+9p^2-6p^2+22p+12-65=0 3p^2-8p-28=0 D=(-8)^2-4*3*(-28)=400 p1=(8-20)/6=-2 p2=(8+20)/6=14/3 Проверим, подставив эти значения "p" в исходное уравнения, чтобы убедиться, что дискриминант неотрицателен. Проверять здесь не буду из-за экономии времени. Все найденные "p" подходят. Теперь найдем корни уравнения: 1)p=-2 x^2-11x+28=0 x1=4; x2=7 2)p=14/3 x^2+9x+8=0 x1=-8; x2=-1 ответ: при p=-2 x1=4, x2=7; при p=14/3 x1=-8, x2=-1.
7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1)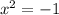
число в корне не может равняться отрицательному числу, корней уравнения нет.
2)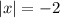
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1)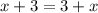
корней уравнения нет.
2)
корней уравнения нет.
=> уравнения равносильные.
9. 1)
ОДЗ: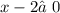 ,
, 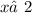 ;
;
ответ: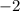
2)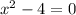
ответ: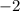 ;
; 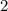
=> уравнения не равносильные.
10. 1)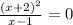
ОДЗ: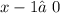 ,
, 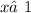 ;
;
ответ: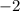
2)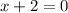
ответ: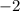
=> уравнения равносильные.
12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12.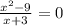
ОДЗ: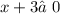 ,
,  ;
;
ответ: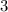
13.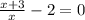
ОДЗ: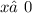 ;
;
ответ: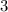
14.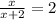
ОДЗ: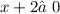 ,
,  ;
;
ответ: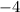
15.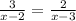
ОДЗ: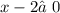 ,
, 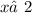 ,
, 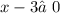 ,
, 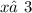 ;
;
ответ:
16.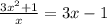
ОДЗ: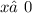 ;
;
ответ: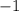
(3p-5)^2-4(3p^2-11p-6)>=0. При таких "p" у исходного уравнения найдутся(возможно, совпадающие) корни x1 и x2. Запишем для них теорему Виета:
x1+x2=-b/a=5-3p
x1*x2=c/a=3p^2-11p-6
Теперь,не вычисляя корней, можно найти сумму их квадратов через "p": x1^2 + x2^2.
Выделим полный квадрат:
(x1+x2)^2-2x1*x2= (5-3p)^2-2(3p^2-11p-6).
По условию, эта сумма квадратов равна 65.
Получаем:
(5-3p)^2-2(3p^2-11p-6)=65
Решим его:
25-30p+9p^2-6p^2+22p+12-65=0
3p^2-8p-28=0
D=(-8)^2-4*3*(-28)=400
p1=(8-20)/6=-2
p2=(8+20)/6=14/3
Проверим, подставив эти значения "p" в исходное уравнения, чтобы убедиться, что дискриминант неотрицателен.
Проверять здесь не буду из-за экономии времени. Все найденные "p" подходят.
Теперь найдем корни уравнения:
1)p=-2
x^2-11x+28=0
x1=4; x2=7
2)p=14/3
x^2+9x+8=0
x1=-8; x2=-1
ответ: при p=-2 x1=4, x2=7; при p=14/3 x1=-8, x2=-1.