Объяснение:
Разложим выражение на множители, для чего найдем корни квадратного трехчлена, используя формулу дискриминанта:
Так как то
Если или такое неравенство будет иметь решение в виде интервала.
При т. е. неравенство не будет иметь решений.
Объяснение:
Разложим выражение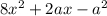 на множители, для чего найдем корни квадратного трехчлена, используя формулу дискриминанта:
на множители, для чего найдем корни квадратного трехчлена, используя формулу дискриминанта:
Так как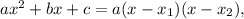 то
то
Если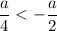 или
или 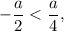 такое неравенство будет иметь решение в виде интервала.
такое неравенство будет иметь решение в виде интервала.
При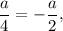 т. е.
т. е. 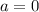 неравенство не будет иметь решений.
неравенство не будет иметь решений.