При -2<x≤2, графиком функции f(x) будет y=3-x². Это парабола, ветви направлены вниз, координата вершины (0;3). Найдём точки пересечения с осями координат:
x=0 ⇒ y=3-0²=3; (0;3)
y=0 ⇒ 3-x²=0; x²=3; x=±√3; (-√3;0), (√3;0).
Всё, что мы нашли находится в указанном промежутке. 3-(-2)²=3-2² - ординаты границ промежутка совпадают, период равен 4 ⇒ 2-4 = -2, поэтому график функции f(x) будет непрерывным. Таблицу точек для y=3-x² и график функции смотри в приложении.
б)
Нули для y=3-x² мы знаем, для f(x) будут такие же нули, но есть ещё период, поэтому - ответ.
Нам в школе давали подобные примеры и говорили: Группировать лучше так, чтобы выходили одинаковые начала в квадратном уравнении. Поясняю: Сгруппировать (x+1)(x+4)(x+2)(x+3) намного приятней. Сейчас покажу, почему:
(x+1)(x+4)(x+2)(x+3) = 5040 Раскрываем скобки: (не забывай, мы раскрываем две скобки, а не все сразу, мало ли, у меня такое было на практике) (+5x+4)(+5x+6)=5040
Видим здесь одинаковое выражение: +5x
Замена: +5x = t
(t+4)(t+6)=5040 Раскрываем скобки. + 10t + 24 = 5040 Решаем как обычное квадратное уравнение, только в корнях вместо x будет t. D = 20164 = √20164 = 142 t1 = 66, t2 = -76
Теперь вернёмся к нашей замене. Выйдет система: 1) +5x = 66 2) +5x = -76
1. Не буду решать, это обычный дискриминант. Напишу ответ: x1 = -11, x2 = 6 2. Дискриминант меньше нуля. Нам в школе говорили, что если дискриминант меньше нуля, то есть два корня: мы вводили мнимую единицу. Но в школе без углубления при условии, что дискриминант меньше нуля - корней нет.
а)
При -2<x≤2, графиком функции f(x) будет y=3-x². Это парабола, ветви направлены вниз, координата вершины (0;3). Найдём точки пересечения с осями координат:
x=0 ⇒ y=3-0²=3; (0;3)
y=0 ⇒ 3-x²=0; x²=3; x=±√3; (-√3;0), (√3;0).
Всё, что мы нашли находится в указанном промежутке. 3-(-2)²=3-2² - ординаты границ промежутка совпадают, период равен 4 ⇒ 2-4 = -2, поэтому график функции f(x) будет непрерывным. Таблицу точек для y=3-x² и график функции смотри в приложении.
б)
Нули для y=3-x² мы знаем, для f(x) будут такие же нули, но есть ещё период, поэтому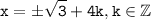
- ответ.
в)
Определим по графику.
Группировать лучше так, чтобы выходили одинаковые начала в квадратном уравнении. Поясняю:
Сгруппировать
(x+1)(x+4)(x+2)(x+3) намного приятней. Сейчас покажу, почему:
(x+1)(x+4)(x+2)(x+3) = 5040
Раскрываем скобки: (не забывай, мы раскрываем две скобки, а не все сразу, мало ли, у меня такое было на практике)
(
Видим здесь одинаковое выражение:
Замена:
(t+4)(t+6)=5040
Раскрываем скобки.
Решаем как обычное квадратное уравнение, только в корнях вместо x будет t.
D = 20164 = √20164 = 142
t1 = 66, t2 = -76
Теперь вернёмся к нашей замене. Выйдет система:
1)
2)
1. Не буду решать, это обычный дискриминант. Напишу ответ:
x1 = -11, x2 = 6
2. Дискриминант меньше нуля. Нам в школе говорили, что если дискриминант меньше нуля, то есть два корня: мы вводили мнимую единицу. Но в школе без углубления при условии, что дискриминант меньше нуля - корней нет.
ответ: x1 = -11, x2 = 6