При котором крупнейшем целом значении a функция f (x) = (а-2) x2 + 2ах + a + 4 имеет два нуля?

Показать ответ

Ответ:

Wolceme

09.08.2021 23:43

Воспользуемся формулой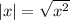 $|x| = \sqrt{x^{2} }$ :

$\sqrt{(2^{x} -2)^{2} } =\sqrt{a^{2} } \\$

Возведем обе части в квадрат:

$(\sqrt{(2^{x} -2)^{2} })^{2} =(\sqrt{a^{2} })^{2} \\ (2^{x} -2)^{2} =a^{2} \\(2^{x} -2)^{2}-a^{2} =0\\(2^{x} -2-a)(2^{x} -2+a) = 0\\$

Рассмотрим 3 случая :

$2^{x} -2-a = 0\\ 2^{x} -2+a \neq 0\\$

----------------------

$2^{x}= 2+a$

Мы знаем, что любое число(кроме 0) в любой степени больше нуля, то есть 2+а > 0 => a>-2

$2^{x} \neq 2-a\\$

Так же 2-а уже должно быть меньше или равно нулю:

2-a ≤ 0 => a ≥ 2

Найдем пересечение => a ≥ 2

По тому же принципу :

$2^{x} -2-a \neq 0 = 2^{x} \neq 2+a = a\leq -2\\2^{x} -2+a=0 = 2^{x}=2-a= a< 2$

Найдем пересечение => a ≤-2

$2^{x} -2-a=2^{x} -2+a\\-a = a\\2a = 0\\a = 0$

----------------------------------------------------------------------

Объединим три ответа => a Є (-∞ ; -2] U [2 ; +∞)

ответ : a Є (-∞ ; -2] U [2 ; +∞) U {0}

P.S это одно из возможных решений, возможно вы найдете и по проще)

0,0(0 оценок)

Ответ:

kamely98

09.08.2021 23:43

f(x)=|x-1|-|x+1|+x
Обзозначим график функции, как ломаную линию с отрезками
[CA]-[AB]-[BD] (cм. чертеж во вложении), где [AB] пересекает точку начала координат О: [AO]=(OB],
[CA] II [BD], т.к. A(-1;1) B(-3;-1)
C(-3;-1) D(3;1)
Вычислим k прямой y=kx, проходящей через точки А и В:
А(-1;1) => 1=k*(-1) => k=-1
Вложение: таблицы и графики
B(1;-1) => -1=k*1 => k=-1
Прямая а, проходящая через точки А,О,В имеет вид у=-х
Прямая b, параллельная [AC] и [BD] и перпендикулярная прямой а,
имеет вид у=х (k=1).
В уравнении у=kx которая имеет с графиком данной функции только одну общую точку, k≠-1; k≠0; k≤1
k∈(-1;0)∪(0;1]

Постройте график функции y=|x-1|-|x+1|+x и найдите все значения k, при которых прямая y=kx имеет с г