Відповідь:
f(x) має дійсни корені при а ∈ (-∞;-7]∪[-3;+∞]
Пояснення:
Рівняння має дійсні корені, коли дискримінант рівняння ≥0.
тому запишемо
D=
тому (а+5)²-4*1≥0;
а²+10а+25-4≥0
а²+10а+21≥0. a1=-10-4/2=-7 a2=-10+4/2=-3
Графіком рівняння а²+10а+21=0 є парабола з точками перетину з віссю ОХ
(-7;0) та (-3;0) вітки параболи направлені догори тому вона буде додатня на відрізках а ∈ (-∞;-7]∪[-3;+∞]
Відповідь: f(x) має дійсни корені при а ∈ (-∞;-7]∪[-3;+∞]
Відповідь:
f(x) має дійсни корені при а ∈ (-∞;-7]∪[-3;+∞]
Пояснення:
Рівняння має дійсні корені, коли дискримінант рівняння ≥0.
тому запишемо
D=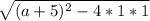
тому (а+5)²-4*1≥0;
а²+10а+25-4≥0
а²+10а+21≥0.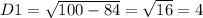 a1=-10-4/2=-7 a2=-10+4/2=-3
a1=-10-4/2=-7 a2=-10+4/2=-3
Графіком рівняння а²+10а+21=0 є парабола з точками перетину з віссю ОХ
(-7;0) та (-3;0) вітки параболи направлені догори тому вона буде додатня на відрізках а ∈ (-∞;-7]∪[-3;+∞]
Відповідь: f(x) має дійсни корені при а ∈ (-∞;-7]∪[-3;+∞]