Нехай - послідовність геометричної прогресії з першим членом і знаменником прогресії . Знаючи, що корені рівняння утворюють геометричну прогресію, то ліву частину рівняння можна представити у наступному вигляді:
Прирівнюючи коефіцієнти при степені , отримаємо
Відповідь: 39.
Нехай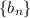 - послідовність геометричної прогресії з першим членом
- послідовність геометричної прогресії з першим членом 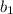 і знаменником прогресії
і знаменником прогресії 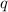 . Знаючи, що корені рівняння
. Знаючи, що корені рівняння 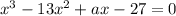 утворюють геометричну прогресію, то ліву частину рівняння можна представити у наступному вигляді:
утворюють геометричну прогресію, то ліву частину рівняння можна представити у наступному вигляді:
Прирівнюючи коефіцієнти при степені , отримаємо
, отримаємо
Відповідь: 39.