ответ: 25
Объяснение:
Рассмотрим треугольник со сторонами 16 и 12, в нем неизвестная сторона будет равна: х==20
Воспользуемся свойством высоты в прямоугольном треугольнике, проведенной из прямого угла:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных ему, каждый из которых подобен данному.
Используя отношение найдем второй катет большого треугольника через маленькие:
, где х=15
Найдем гипотенузу через формулы площади треугольника.
S=, где а=16+х, h=12
а=16+х-гипотенуза
S=, где sin90=1, а=20, b=15.
S==150
150=, а==25.
а) х² - х + 1/4
х может принимать любые действительные значения.
б) (х+1)/(х²+9) + 2х
Знаменатель дроби не должен равняться нулю.
Рассматриваем знаменатель х²+9 и видим, что он всегда больше нуля, поэтому опять:
в) 14\3х-6
Рассматриваем знаменатель 3х - 6 ≠ 0 ⇒ 3х ≠ 6 ⇒ х ≠ 2
х может принимать любые действительные значения, кроме х = 2
г) х²-3/(3-2х)(х+5)
Рассматриваем знаменатель
1) 3 - 2х ≠0 ⇒ -2х ≠ -3 ⇒ х ≠ 1,5
2) х+5 ≠ 0 ⇒ х ≠ -5
х может принимать любые действительные значения, кроме х = 1,5 и х = -5
д)х²+1/х(х+3)
1) х ≠0
2) х+3 ≠ 0 ⇒ х ≠ -3
х может принимать любые действительные значения, кроме х = 0 и х = -3
е) 2х/(х-1)²·(х²-4)
1) х - 1 ≠ 0 ⇒ х ≠ 1
2) х² - 4 ≠ 0 ⇒ х² ≠ 4 ⇒ х ≠ -2 и х ≠ 2
х может принимать любые действительные значения, кроме х = 1, х = -2 и х = 2
ответ: 25
Объяснение:
Рассмотрим треугольник со сторонами 16 и 12, в нем неизвестная сторона будет равна: х=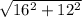 =20
=20
Воспользуемся свойством высоты в прямоугольном треугольнике, проведенной из прямого угла:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных ему, каждый из которых подобен данному.
Используя отношение найдем второй катет большого треугольника через маленькие:
Найдем гипотенузу через формулы площади треугольника.
S=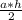 , где а=16+х, h=12
, где а=16+х, h=12
а=16+х-гипотенуза
S=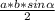 , где sin90=1, а=20, b=15.
, где sin90=1, а=20, b=15.
S=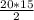 =150
=150
150=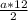 , а=
, а=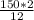 =25.
=25.
а) х² - х + 1/4
х может принимать любые действительные значения.
б) (х+1)/(х²+9) + 2х
Знаменатель дроби не должен равняться нулю.
Рассматриваем знаменатель х²+9 и видим, что он всегда больше нуля, поэтому опять:
х может принимать любые действительные значения.
в) 14\3х-6
Знаменатель дроби не должен равняться нулю.
Рассматриваем знаменатель 3х - 6 ≠ 0 ⇒ 3х ≠ 6 ⇒ х ≠ 2
х может принимать любые действительные значения, кроме х = 2
г) х²-3/(3-2х)(х+5)
Рассматриваем знаменатель
1) 3 - 2х ≠0 ⇒ -2х ≠ -3 ⇒ х ≠ 1,5
2) х+5 ≠ 0 ⇒ х ≠ -5
х может принимать любые действительные значения, кроме х = 1,5 и х = -5
д)х²+1/х(х+3)
Рассматриваем знаменатель
1) х ≠0
2) х+3 ≠ 0 ⇒ х ≠ -3
х может принимать любые действительные значения, кроме х = 0 и х = -3
е) 2х/(х-1)²·(х²-4)
Рассматриваем знаменатель
1) х - 1 ≠ 0 ⇒ х ≠ 1
2) х² - 4 ≠ 0 ⇒ х² ≠ 4 ⇒ х ≠ -2 и х ≠ 2
х может принимать любые действительные значения, кроме х = 1, х = -2 и х = 2