примеры 8 класс и уравнение 8 класс

Объяснение:

1. a - ширина прямоугольника, см.

Площадь прямоугольника: S=ab.

21=a(a+7)

a²+7a-21=0; D=49+84=133

a₁=(-7-√133)/2 - так как a₁<0, то этот корень не подходит по смыслу к данной задаче.

a₂=(-7+√133)/2 см - ширина прямоугольника.

b₂=(-7+√133)/2 +7=(-7+14+√133)/2=(7+√133)/2 см - длина прямоугольника.

Периметр прямоугольника:

P=2(a+b)=2((-7+√133)/2 +(7+√133)/2)=2√133 см

2.

x - скорость байдарки, км/ч.

8/(x-3) +10/(x+3)=3

8(x+3)+10(x-3)=3(x-3)(x+3)

8x+24+10x-30=3(x²-9)

3x²-27-18x+6=0

3x²-18x-21=0    |3

x²-6x-7=0

x₁+x₂=6; 7-1=6

x₁x₂=-7; 7·(-1)=-7

x₁=7 км/ч - скорость байдарки.

x₂=-1 - этот корень не подходит по смыслу к данной задаче.

7-3=4 км/ч - скорость байдарки против течения.

Произведение равняется нулю, когда хотя бы один один из множителей равняется нулю.

В данном случае множителей два:

первый: , а второй: .

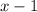Поэтому мы их и приравниваем по очереди к нулю, то есть:

1)

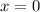
2)

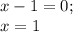
Если икс будет равен нулю или единице, то мы точним получим ноль в решении.

Замечу, что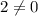 (это - разные числа), следовательно, правило, описанное выше, не подходит. Оно подходит только (!) если после равно стоит ноль и выполняется действие умножения (а не вычетаниея, как, например, записано чуть ниже, сложения или деления).

Это уравнение решается таким

1) переносим двойку в левую часть с противоположным знаком (был "+", перенесли, стал "-")

(тут у нас уже НЕ умножение, а вычетание, т.к. мы отнимаем двойку, значит, тот метод НЕ подходит)

Раскрываем скобки:

По теореме Виета для уравнения:

То есть для нашего уранвения:

Подбираем их, вспоминая таблицу умножения. Такими числами являются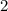 и .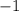

Действительно:

Cледовательно