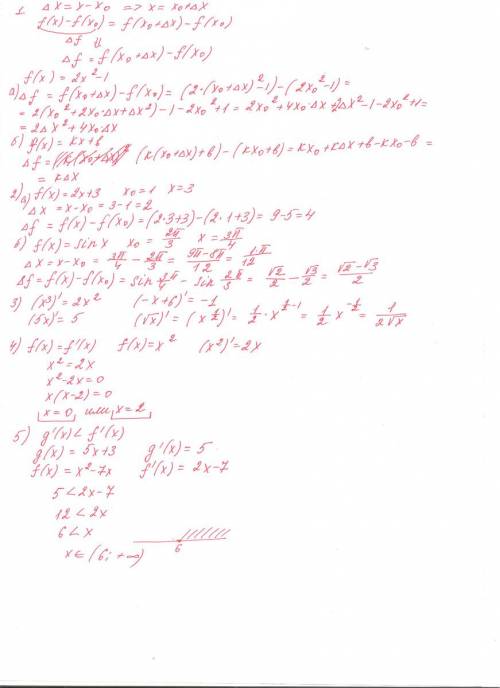Приращение функции. понятие о производной и непрерывности функций. 10 класс. 1. выразите приращение функции f в точке x₀ через x₀ и δx, если: а) f(x)=2x²- 1 ; б) f(x)= kx+b. 2. найдите приращение δx и δf в точке х₀, если: a) f(x)=2x+3; x₀=1; x=3; б) f(x)= sin x; x₀ = 2п/3; x= 3п/4. 3. найти производные: a) (x³)' ; б) (5х)' ; в) (-x+6)' ; г) (√x)'. 4. решите уравнение f(x) = f '(x), если f(x) = x². выберите верный из предложенных ответов. а)0; 2 б)2; -2 в)0; -2 5. определите, при каких значениях х выполняется неравенство g'(x) < f '(x), если g(x)= 5x+3, f(x)= x²-7x.