Приведите уравнение (3х – 1) (х-2) =х(х-4) к стандартному виду aх2 +bх+c=0. Запишите коэффициенты квадратного уравнения и определите вид уравнения. [2]
2. Определите, какое из перечисленных ниже уравнений является
приведенным квадратным уравнением:
A) -2х2-4х+13=0
B) -12х2=3х
C) у2+у=2у+1
D) 13+2х2-3х=0
E) t2-16t=9 [1]
3. Найдите все такие значения х, при которых выражения
2(х² - 2) и (х - 2)(х + 2) принимают равные значения. [3]
4. Если х₁ и х₂ - корни уравнения х² + 4х – 5 = 0, то найдите значение выражения[3]
5. Для квадратного трехчлена х2 + 6х - 7
а) выделите полный квадрат;
b) разложите квадратный трехчлен на множители. [3]
6. Решите уравнение: x2 – 7|x| + 6 = 0. [4]
тому кто все решить
ответ: 1/6
Объяснение: для начала выведем формулу самой прямой.
Пусть прямая, проходящая через заданные точки, имеет вид у = kx + b.
По условию y(1) = 0, y(0) = -3.
1)1 · k + b =0, k + b = 0 ⇒ k = -b.
2)0·k + b = -3. b = -3 ⇒ k = 3.
Исходная прямая - y = 3x - 3.
Теперь исследуем функцию y = -x² + 4x - 3. График - парабола, ветви направлены вниз.
Нули функции - x = 1 и x = 3. Вершина: x = -b/2a = -4/-2=2, y=-2²+8-3=-4+5=1. (2; 1) Нам этого достаточно.
Строим графики (во вложении. Фигура, площадь которой нужно найти, заштрихована красным).
Площадь фигуры будем искать на отрезке [0; 1]
По формуле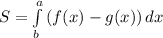
где f(x) ≥ g(x) (т.е. график функции f выше графика функции g) находим искомую площадь:
Искомая площадь - S = 1/6 (кв. ед)
Объяснение:
1.
a) 4x³+x+2+6x³-2x²-1=10x³-2x²+x+1.
b) 4x³+x+2-(6x³-2x²-1)==4x³+x+2-6x³+2x²+1=-2x³+2x²+x+3.
2.
a) 3x⁵*(1-x²)=⁵-3x⁷.
b) (a+5)(a-3)=a²-3a+5a-15=a²+2a-15.
3.
((x+15)/3)-((7x+4)/8)=4 |×24
8*(x+15)-3*(7x+4)=4*24
8x+120-21x-12=96
-13x+108=96
13x=12 |÷13
x=12/13.
4.
(a-3)(a+4)-(a+5)(a+1)=a²+a-12-(a²+6a+5)=a²+a-12-a²-6a-5=
=-5a-17=-5*(-1/3)-17=-(-5/3)-17=1²/₃-17=-15¹/₃.
5.
Пусть первое число - х.
1. Второе число - х+1.
2.Третье число х+2. ⇒
(x+1)(x+2)-x²=17
x²+x+2x+2-x²=17
3x²=17-2
3x=15 |÷3
x=5.
ответ: 5; 6; 7.