С монетой все проще. У монеты две стороны. Вероятность того, что монета упадет на ребро столь мала, что это не берется в расчет и целые доли округляются в борльшую сторону, то есть 0.5, так как орел только с одной стороны, бросаем монету один раз, следовательно и шанс 1 из 2, то есть , то есть 0.5
Объяснение:
2)-x²+x+72>0
x²-x-72=0
х₁,₂=(1±√1+288)/2
х₁,₂=(1±√289)/2
х₁,₂=(1±17)/2
х₁= -16/2= -8
х₂=18/2=9
x∈(-8; 9)
Решения неравенства находятся в области от -8 до 9.
4)x²+x-210<=0
x²+x-210=0
х₁,₂=(-1±√1+840)/2
х₁,₂=(-1±√841)/2
х₁,₂=(-1±29)/2
х₁= -30/2= -15
х₂=28/2=14
x∈(-15; 14)
Решения неравенства находятся в области от -15 до 14.
6)25x²+90x+81<=0
25x²+90x+81=0
х₁,₂=(-90±√8100-8100)/50
х₁,₂=(-90±√0)/50
х₁,₂= -90/50= -9/5
x> -9/5
8)36x²-84x+49>0
36x²-84x+49=0
х₁,₂=(84±√7056-7056)/72
х₁,₂=(84±√0)/72
х₁,₂=84/72=7/6
x<7/6
4 пули 4 выстрела
P1(A)=0.6 P(т)=1-0.6=0.4
P2(тA)=0.6*0.4=0.24
P3(ттA)=0.6*0.4^2=0.096
P4(ttt)=0.4^3=0.064
Складываем вероятности
0.064+0.096+0.24+0.6=1
Х 1 2 3 4
Р 0.6 0.24 0.096 0.063
С монетой все проще. У монеты две стороны. Вероятность того, что монета упадет на ребро столь мала, что это не берется в расчет и целые доли округляются в борльшую сторону, то есть 0.5, так как орел только с одной стороны, бросаем монету один раз, следовательно и шанс 1 из 2, то есть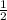
, то есть 0.5
Х 0 1
Р 0.5 0.5