Проведен опыт – два бросания игральной кости. На диаграмме Эйлера отметили точками все возможные элементарные события этого опыта. Пусть событие А – «на первой кости выпало 6 очков», событие В – «на второй кости выпало 3 очка».
Заполните таблицу.
Сколько точек попало внутрь круга, изображающего событие А?
Сколько точек попало внутрь круга, изображающего событие В?
Сколько точек попало внутрь общей части кругов, изображающих события А и В?
Сколько точек попало внутрь фигуры, изображающей объединение событий А и В?
Сколько точек попало внутрь фигуры, изображающей пересечение событий А и В?
И она в нужном месте! Каждый товар в этом магазине уникален!
Это задача на классическое правило умножения:
Если объект
------------------------------------------------
Нужно последовательно одно за другим осуществить три действия (в любом порядке): выбор КАРАНДАША, выбор РУЧКИ, выбор ТЕТРАДИ.
Пусть сначала выбирается карандаш, потом ручка, потом тетрадь:
- первое действие можно осуществить И ПРИ ЛЮБОМ ЕГО ОСУЩЕСТВЛЕНИЯ второе действие можно осуществить и в конце ПРИ ЛЮБОМ ОСУЩЕСТВЛЕНИЯ ПЕРВЫХ ДВУХ ДЕЙСТВИЙ третье действие можно осуществить
Тогда эти три действия можно осуществить
ответ:
На числовой прямой:
t и -t
Числа имеют противоположные знаки и |t| = |-t|. Точки симметричны относительно нуля.
t и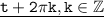
k=0 ⇒ точки совпадают.
k<0 ⇒ t правее t+2πk на 2πk
k>0 ⇒ t левее t+2πk на 2πk.
t и t+π
t левее t+π на π.
t+π и t-π
t+π правее t-π на 2π.
На числовой окружности:
t и -t
Точки симметричны относительно оси абсцисс (Ox).
t и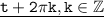
Точки совпадают т.к. 2π это целый круг.
t и t+π
Точки симметричны относительно начала координат т.к. π это половина круга.
t+π и t-π
Точки совпадают т.к. они различаются на 2π, а это целый круг.