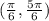Если вещественная функция, непрерывная на отрезке и дифференцируемая на интервале , принимает на концах отрезка одинаковые значения, то на интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
Условия теоремы выполняются, функция непрерывна и дифференцируема, на концах принимает одинаковые значения
Найдем производную.
Производная обращается в ноль в точке , которая принадлежит интервалу
Объяснение:
Теорема Ролля утверждает.
Если вещественная функция, непрерывная на отрезке![{\displaystyle [a,b]}](/tpl/images/1464/4311/72c4a.png) и дифференцируемая на интервале
и дифференцируемая на интервале 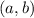 , принимает на концах отрезка
, принимает на концах отрезка ![{\displaystyle [a,b]}](/tpl/images/1464/4311/72c4a.png) одинаковые значения, то на интервале
одинаковые значения, то на интервале 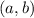 найдётся хотя бы одна точка, в которой производная функции равна нулю.
найдётся хотя бы одна точка, в которой производная функции равна нулю.
Условия теоремы выполняются, функция непрерывна и дифференцируема, на концах принимает одинаковые значения
Найдем производную.
Производная обращается в ноль в точке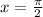 , которая принадлежит интервалу
, которая принадлежит интервалу