Проверяющий олимпиады после тяжёлого трудового дня покидает рабочий кабинет, освен щение в котором работает в нескольких режимах. Когда проверяющий вышел из комна-
ты, он плотно закрыл за собой дверь и встал у кнопки, которая переключает эти режимы
(режимы переключаются по порядку от первого до последнего, после последнего идет
выключение, а затем все заново). Но, к сожалению, проверяющий очень устал и забыл
точное количество режимов, а помнит лишь, что их было не больше 5 (не считая вы-
ключенного состояния) и что сейчас включён первый режим проверяющему
выключить свет в кабинете, если он не может видеть, какой режим включён
По условию известно, что режимов освещения было не больше 5. То есть их могло быть:
1, 2, 3, 4, 5
Так как существует также полное отключение освещения, всего состояний может быть:
2, 3, 4, 5, 6
Найдем, сколько раз нужно нажать на кнопку, чтобы независимо от точного количества режимов вернуться в тот же самый режим. Для этого, нужно найти число, которое делится на 2, 3, 4, 5, 6 без остатка. То есть, другими словами нужно найти НОК этих чисел.
Таким образом, если нажать на кнопку 60 раз, то мы перейдем к такому же состоянию, с которого все начиналось.
По условию сейчас включен первый режим, также известно, что именно перед первым режимом идет состояние полного отключения. Значит, нажав на кнопку 60 раз мы вернемся к первом режиму, а если мы нажмем на кнопку на 1 раз меньше, то есть 59 раз, то мы полностью выключим свет.
Найденный является простейшим с той точки зрения, что нажать на кнопку можно и большее количество раз, а именно любое количество, задаваемое формулой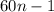 , где
, где 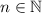 , и свет также будет отключен.
, и свет также будет отключен.
ответ: нажать на кнопку 59 раз