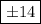Корень пятой степени равен -2 возведем обе части в степень 5. 2x-7=(-2)^5=-32 2x=-32+7=-25 x=12.5
выражение в знаменателе ≠0 5х-8≠0 х≠8/5 5х-8>0← под корнем число большее 0 →x>8/5
t+5=√(2t²+19t+43) t+5≥0 → t≥-5 возводим обе части в квадрат → t²+10t+25=2t²+19t+43→ t²+9t+18=0 корни по виетту t1=-3 t2=-6 этот корень меньше -5 и не годится. ответ -3
разность дробей в примере 4 находим используя формулу разности квадратов. (2х^0.5-3y^0.5-2x^0.5-3y^0.5)/(4x^1-9y^1)=-6y^0.5/(4x-3y) умножим -6y^0.5*(2x-9y/2)/(4x-9y)=-6y^0.5(4x-9y)/2(4x-9y)=-3y^0.5= =-3√y
Попробуем в левой части выделить полный квадрат, как раз от выражения
Здесь удвоенное произведение я искусственно создал для выделения квадрата, но чтобы не нарушить равенства, надо это же удвоенное произведение с противоположным знаком добавить, что и было сделано.
Было получено два значения и не зря. Если решать уравнение из условия, то мы обязательно получим 2 корня (кроме случая x=0, на котором даже не определено второе слагаемое и потому его в расчет не берем), это и второе выражение, которое зависит от этих корней, может и будет принимать не одно лишь значение, а 2.
2x-7=(-2)^5=-32 2x=-32+7=-25 x=12.5
выражение в знаменателе ≠0 5х-8≠0 х≠8/5
5х-8>0← под корнем число большее 0 →x>8/5
t+5=√(2t²+19t+43)
t+5≥0 → t≥-5
возводим обе части в квадрат → t²+10t+25=2t²+19t+43→
t²+9t+18=0 корни по виетту t1=-3 t2=-6 этот корень меньше -5 и не годится.
ответ -3
разность дробей в примере 4 находим используя формулу разности квадратов.
(2х^0.5-3y^0.5-2x^0.5-3y^0.5)/(4x^1-9y^1)=-6y^0.5/(4x-3y)
умножим -6y^0.5*(2x-9y/2)/(4x-9y)=-6y^0.5(4x-9y)/2(4x-9y)=-3y^0.5=
=-3√y
Попробуем в левой части выделить полный квадрат, как раз от выражения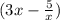
Здесь удвоенное произведение я искусственно создал для выделения квадрата, но чтобы не нарушить равенства, надо это же удвоенное произведение с противоположным знаком добавить, что и было сделано.
Было получено два значения и не зря. Если решать уравнение из условия, то мы обязательно получим 2 корня (кроме случая x=0, на котором даже не определено второе слагаемое и потому его в расчет не берем), это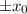 и второе выражение, которое зависит от этих корней, может и будет принимать не одно лишь значение, а 2.
и второе выражение, которое зависит от этих корней, может и будет принимать не одно лишь значение, а 2.
ответ: