Уравнение второго порядка - парабола - у= х², но со смещенным началом координат. Надо найти эту точку упростив уравнение. ДАНО у = х²+4х+3 = 0 РЕШЕНИЕ Надо привести уравнение к виду y = (х+a)² + b Используем правило, что можно прибавить и вычесть одно и тоже выражение и равенство не изменится. y = x² + 2*2x + 2² - 4 + 3 = 0 y = (x+2)² - 1. Координата начала параболы х= -2 и у = -1 - Строим обычную параболу у=х² с началом в этой точке. ВРЕДНЫЙ СОВЕТ - так не надо решать задачу. Чтобы решить графически надо решить алгебраически. Решаем квадратное уравнение и получаем корни - х1 = -1 и х2 =3 и при х=0 - у(0) = 3. Теперь можно и график построить.
Формула сложной процентной ставки: , где S - наращенная сумма, P - первоначальная сумма вклада, i - процентная ставка, n - срок ссуды;
Само решение:
Пусть клиент сначала положил x грн в банк, тогда через год он получит грн и получил он прибыль 100 грн, т.е. откуда
К общей сумме он добавил 400 грн на год свои сбережения в банке, то на следующий год он получит грн, что по условию вклад вместе с процентами составил 1650 грн.
Решаем как квадратное уравнение через дискриминант
грн - начальная сумма вклада
грн - не подходит условию, так как клиент положил несколько 100 гривневых купюр
ответ: начальная сумма вклада 1000 грн с 10% годовыми.
ДАНО
у = х²+4х+3 = 0
РЕШЕНИЕ
Надо привести уравнение к виду
y = (х+a)² + b
Используем правило, что можно прибавить и вычесть одно и тоже выражение и равенство не изменится.
y = x² + 2*2x + 2² - 4 + 3 = 0
y = (x+2)² - 1.
Координата начала параболы х= -2 и у = -1 -
Строим обычную параболу у=х² с началом в этой точке.
ВРЕДНЫЙ СОВЕТ - так не надо решать задачу.
Чтобы решить графически надо решить алгебраически.
Решаем квадратное уравнение и получаем корни - х1 = -1 и х2 =3 и при х=0 - у(0) = 3.
Теперь можно и график построить.
Формула сложной процентной ставки: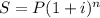 , где S - наращенная сумма, P - первоначальная сумма вклада, i - процентная ставка, n - срок ссуды;
, где S - наращенная сумма, P - первоначальная сумма вклада, i - процентная ставка, n - срок ссуды;
Само решение:
Пусть клиент сначала положил x грн в банк, тогда через год он получит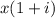 грн и получил он прибыль 100 грн, т.е.
грн и получил он прибыль 100 грн, т.е. 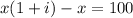 откуда
откуда 
К общей сумме он добавил 400 грн на год свои сбережения в банке, то на следующий год он получит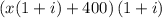 грн, что по условию вклад вместе с процентами составил 1650 грн.
грн, что по условию вклад вместе с процентами составил 1650 грн.
Решаем как квадратное уравнение через дискриминант
ответ: начальная сумма вклада 1000 грн с 10% годовыми.