Пусть скорость пешехода равна х км/ч, а велосипедиста - у км/ч. Пешеход и велосипедист встретились через 2 часа после выезда, поэтому . После встречи пешеход прибыл в пункт Б на 5 ч20 мин позже, чем велосипедист в пункт А, поэтому
5ч 20мин = 5 + (20/20) = 5 + (1/3) = 16/3
Составим и решим систему уравнений
Умножим левую и правую части уравнения на 3y(16-y)/16≠0, имеем
По теореме Виета
— не удовлетворяет условию;
км/ч — скорость велосипедиста
Скорость пешехода равна 16 - 12 = 4 км/ч.
ответ: скорость пешехода - 4 км/ч и скорость велосипедиста - 12 км/ч
Аименьшее целое решение - 0. 1) правая часть отрицательна, тогда подкоренное выражение неотрицательно (кв.корень всегда больше отрицательного числа, если корень имеет смысл), система: -x<0, x+2>=0;
x>0, x>=-2;
x>0.
2)правая часть неотрицательна, возводим в квадрат, получаем систему: x+2>x^2, -x>=0;
x^2-x-2<0, x<=0;
(x+1)(x-2)<0, x<=0 Промежуток от -1 до 2 в первом неравенстве и от -бесконечности до нуля во втором. Пересечение (-1;0]. Наименьшее целое решение - 0.
Пусть скорость пешехода равна х км/ч, а велосипедиста - у км/ч. Пешеход и велосипедист встретились через 2 часа после выезда, поэтому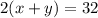 . После встречи пешеход прибыл в пункт Б на 5 ч20 мин позже, чем велосипедист в пункт А, поэтому
. После встречи пешеход прибыл в пункт Б на 5 ч20 мин позже, чем велосипедист в пункт А, поэтому 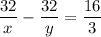
5ч 20мин = 5 + (20/20) = 5 + (1/3) = 16/3
Составим и решим систему уравнений
Умножим левую и правую части уравнения на 3y(16-y)/16≠0, имеем
По теореме Виета
Скорость пешехода равна 16 - 12 = 4 км/ч.
ответ: скорость пешехода - 4 км/ч и скорость велосипедиста - 12 км/ч
1) правая часть отрицательна, тогда подкоренное выражение неотрицательно (кв.корень всегда больше отрицательного числа, если корень имеет смысл), система:
-x<0,
x+2>=0;
x>0,
x>=-2;
x>0.
2)правая часть неотрицательна, возводим в квадрат, получаем систему:
x+2>x^2,
-x>=0;
x^2-x-2<0,
x<=0;
(x+1)(x-2)<0,
x<=0
Промежуток от -1 до 2 в первом неравенстве и от -бесконечности до нуля во втором. Пересечение (-1;0].
Наименьшее целое решение - 0.