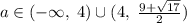Пусть f(x) = l a - 4 | х² + 4х + а - 5. Найдите, при каких значениях параметра а уравнение f(x) = 0 имеет ровно различных 2 решения, причем каждое из этих решений не превосходит единицы.
Пусть — решения уравнения . По условию . Можно сделать замену: и рассмотреть функцию . Переформулируем условие: найти все значения параметра , при каждом из которых уравнение имеет два различных неположительных решения.
, после преобразований получим . Необходимым и достаточным условием неположительности решений явлется неположительность суммы и неотрицательность произведения корней. Применяя теорему Виета, переходим к системе: . Сразу заметим, что не подходит, так как дает уравнение с не более чем одним решением. Система эквивалентна следующей: (1)
Теперь нужно наличие двух различных решений. Здесь удобно вернутся к изначальному уравнению (так как мы просто двигали параболу горизонтально). , это неравенство эквивалентно системе: (2).
Пусть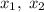 — решения уравнения
— решения уравнения 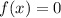 . По условию
. По условию 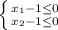 . Можно сделать замену:
. Можно сделать замену: 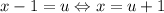 и рассмотреть функцию
и рассмотреть функцию 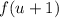 . Переформулируем условие: найти все значения параметра
. Переформулируем условие: найти все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение 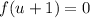 имеет два различных неположительных решения.
имеет два различных неположительных решения.
Теперь нужно наличие двух различных решений. Здесь удобно вернутся к изначальному уравнению (так как мы просто двигали параболу горизонтально).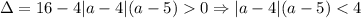 , это неравенство эквивалентно системе:
, это неравенство эквивалентно системе: 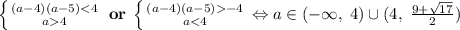 (2).
(2).
Пересекая (1) с (2) получим ответ.
ответ: