Y=-8x/(x²+4). 1) Так как x²+4>0 при любых значениях x, то функция определена при любых х, т.е. областью определения является вся числовая ось. 2) При x=0 y=0, т.е график пересекает координатные оси в начале координат. Других точек пересечения с осями координат нет. 3) y(-x)=-y(x), так что функция является нечётной и потому её можно исследовать только при x≥0. 4) Функция непрерывна на всей числовой оси. lim y при x⇒+∞=0. Таким образом, ось ОХ является горизонтальной асимптотой. Других асимптот нет. 5) y'=(-8*(x²+4)+8x*2x)/(x²+4)²=(8x²-32)/(x²+4)²=8*(x²-4)/(x²+4)², откуда видно, что , т.е. производная обращается в 0 при x=2 и при x=-2. При x<-2 y'>0, при -2<x<2 y'<0, при x>2 y'>0. Отсюда ясно, что точка x=-2 есть точка максимума, равного y(-2)=16/(4+4)=2, а точка x=2 есть точка минимума, равного y(2)=-16/(4+4)=-2. Эти значения одновременно являются соответственно наибольшим и наименьшим значениями функции на всей области определения.
Объяснение:
х км/ч - скорость катера в стоячей воде;
(x-2) км/ч - скорость катера против течения;
(x+2) км/ч - скорость катера по течению;
20/(x+2) ч - время, пройденное по течению;
8/(x-2) ч - время, пройденное против течения.
На весь путь катер затратил 2 часа, составим уравнение
Домножив обе части уравнения на 0.5(x+2)(x-2), получаем
10(x-2) + 4(x+2) = (x+2)(x-2)
10x - 20 + 4x + 8 = x² - 4
x² - 14x + 8 = 0
D = 14² - 4 * 1 * 8 = 164
Корень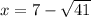
не удовлетворяет условию.
1) Так как x²+4>0 при любых значениях x, то функция определена при любых х, т.е. областью определения является вся числовая ось.
2) При x=0 y=0, т.е график пересекает координатные оси в начале координат. Других точек пересечения с осями координат нет.
3) y(-x)=-y(x), так что функция является нечётной и потому её можно исследовать только при x≥0.
4) Функция непрерывна на всей числовой оси. lim y при x⇒+∞=0. Таким образом, ось ОХ является горизонтальной асимптотой. Других асимптот нет.
5) y'=(-8*(x²+4)+8x*2x)/(x²+4)²=(8x²-32)/(x²+4)²=8*(x²-4)/(x²+4)², откуда видно, что , т.е. производная обращается в 0 при x=2 и при x=-2. При x<-2 y'>0, при -2<x<2 y'<0, при x>2 y'>0. Отсюда ясно, что точка x=-2 есть точка максимума, равного y(-2)=16/(4+4)=2, а точка x=2 есть точка минимума, равного y(2)=-16/(4+4)=-2. Эти значения одновременно являются соответственно наибольшим и наименьшим значениями функции на всей области определения.