Пусть U={x|0<x<8,xєZ}A={x|2<x<7,xєZ} B={x|5<x<8,xєZ}.Найдите: 1)A
2)A¹
3)B
4)B¹
5)A n B
6)A u B
7)A¹ n B¹

ответ: Подпишитесь на мой канал в ютубе

Объяснение:

По определению, функция является четной, если ее область определения симметрична относительно начала координат, и у(- х) = у(х). Если же у(- х) = - у(х), то такая функция будет нечетной.

Найдем область определения функции y = tg 3x. Так как tg 3x = sin 3x / cos 3x, то cos 3x ≠ 0, следовательно,

3х ≠ П/2 + Пn, n – из множества Z.

x ≠ П/6 + Пn/3, n – из множества Z.

Таким образом, область определения функции D(y): все числа, кроме x ≠ П/6 + Пn/3, n – из множества Z – симметрична относительно 0.

у(- х) = tg (3 * (- x)) = tg (- 3x) = - tg 3x = - (y(x)), следовательно, данная функция является нечетной.

Кусочная функция  на графике  нарисована сплошными линиями .

Рисуем параболу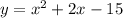     при изменении переменной "х" в пределах от  -3 до 3 ,  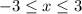  .  Ветви параболы направлены вверх, вершина параболы находится в точке (-1;-16) . Точки (3;0)  и (-3;-12) принадлежат графику .

Прямую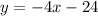     рисуем при  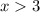  . Точка (3;0) не принадлежит графику .

Прямую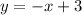     рисуем при  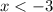  .  Точка (-3;-12) не принадле-жит графику .

  при    .

б)  область значений функции:    ,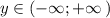

    при   х=5  значение функции  у=-2  ,    .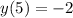

в)   пересечение с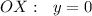     при    ,    .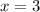

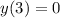     пересечение с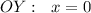    ,  если    .

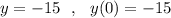г)  y(x) возрастает при    .

    y(x) убывает при    ,