Если на оси ординат (ось ОУ) отмечен единичный отрезок ( от 0 до 1 ) и этот отрезок разделён на 5 частей (отрезок содержит 5 клеток), то надо найти так называемую цену деления одной такой части (цена деления показывает сколько единиц измерения содержится между двумя соседними делениями, то есть это разность между двумя соседними делениями шкалы).
Длина отрезка между 0 и 1 равна 1, отрезок разделён на 5 частей, значит одна часть - это 1/5 от единицы, то есть цена деления равна 1/5.
Если надо определить, какое число соответствует третьему делению, считая от 0, то это будет 3*(1/5)=3/5 (три пятых).
Как и в предыдущей твоей задаче, комплексное число a+bi можно рассматривать как вектор . Как видно из сложения векторов по правилу параллелограмма, сумма двух векторов, имеющих общее начало, является диагональю параллелограмма, двумя сторонами которого являются начальные векторы. Диагональ параллелограмма — это биссектриса его угла. Значит, конец любого вектора, лежащего на луче, продолжающем диагональ параллелограмма, подходит для ответа.
d = 6+8i + 4-3i = 10 + 5i
Вектор v, соответствующий d — (10; 5). Любая точка (n;m) такая, что существует такое неотрицательное число k такое, что k*d = (n;m), лежит на биссектрисе.
Если на оси ординат (ось ОУ) отмечен единичный отрезок ( от 0 до 1 ) и этот отрезок разделён на 5 частей (отрезок содержит 5 клеток), то надо найти так называемую цену деления одной такой части (цена деления показывает сколько единиц измерения содержится между двумя соседними делениями, то есть это разность между двумя соседними делениями шкалы).
Длина отрезка между 0 и 1 равна 1, отрезок разделён на 5 частей, значит одна часть - это 1/5 от единицы, то есть цена деления равна 1/5.
Если надо определить, какое число соответствует третьему делению, считая от 0, то это будет 3*(1/5)=3/5 (три пятых).
Смотри рисунок.
Как и в предыдущей твоей задаче, комплексное число a+bi можно рассматривать как вектор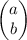 . Как видно из сложения векторов по правилу параллелограмма, сумма двух векторов, имеющих общее начало, является диагональю параллелограмма, двумя сторонами которого являются начальные векторы. Диагональ параллелограмма — это биссектриса его угла. Значит, конец любого вектора, лежащего на луче, продолжающем диагональ параллелограмма, подходит для ответа.
. Как видно из сложения векторов по правилу параллелограмма, сумма двух векторов, имеющих общее начало, является диагональю параллелограмма, двумя сторонами которого являются начальные векторы. Диагональ параллелограмма — это биссектриса его угла. Значит, конец любого вектора, лежащего на луче, продолжающем диагональ параллелограмма, подходит для ответа.
d = 6+8i + 4-3i = 10 + 5i
Вектор v, соответствующий d — (10; 5). Любая точка (n;m) такая, что существует такое неотрицательное число k такое, что k*d = (n;m), лежит на биссектрисе.
Таким образом, n/m = 10/5 = 2.
ответ: {(n+mi) | n/m = 2}