х²-х-90=0
Д=(-1)²-4*1*(-90)=361=19²
х₁= х₂=
х²+6х+9=0
Д=6²-4*9=0
х=
5х²+4х+7=0
Д=4²-4*5*7=-124≤0
коренів не має
х²+2х-35=0
Д=2²-4*(-35)=144=12²
***
квадратное уравнение — это уравнение вида ax² + bx + c = 0,
где
a — первый коэффициент, не равный нулю
b — второй коэффициент
c — свободный член.
решаем с дискриминанта:
1) x² - x - 90 = 0
a = 1, b = -1, c = -90
D = b² - 4ac = (-1)² - 4 · 1 · (-90) = 361 >0
т.к. дискриминант больше нуля, то квадратное уравнение имеет два различных действительных корня
=>
X₁ = (-b+√D) / 2a = ( -(-1) + √361 ) / 2 · 1 = 1 + 19 / 2 = 20/2 = 10
X₂ = (-b-√D) / 2a = ( -(-1) - √361 ) / 2 · 1 = 1 - 19 / 2 = -18/2 = -9
2) x² + 6x + 9 = 0
a = 1, b = 6, c = 9
D = b² - 4ac = (6)² - 4 · 1 · 9 = 36 - 36 = 0
т.к. дискриминант равен нулю, то квадратное уравнение имеет только один действительный корень
X₁,₂ = (-b±√D) / 2a = ( (-6) ±√D ) / 2
3) 5x² + 4x + 7 = 0
a = 5, b = 4, c = 7
D = b² - 4ac = (4)² - 4 · 5 · 7 = 16 - 140 = - 124 < 0
т.к. дискриминант меньше нуля, значит не существует вещественных корней, а только комплексные корни
4) x² + 2x - 35 = 0
a = 1, b = 2, c = -35
D = b² - 4ac = (2)² - 4 · 1 · (-35) = 4 - (-140) = 4 + 140 = 144
X₁ = (-b+√D) / 2a = ( (-2) + √144 ) / 2 · 1 = (-2 + 12) / 2 = 10/2 = 5
X₂ = (-b-√D) / 2a = ( (-2) - √144 ) / 2 · 1 = (-2 - 12) / 2 = -14/2 = -7
х²-х-90=0
Д=(-1)²-4*1*(-90)=361=19²
х₁=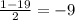 х₂=
х₂=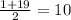
х²+6х+9=0
Д=6²-4*9=0
х=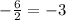
5х²+4х+7=0
Д=4²-4*5*7=-124≤0
коренів не має
х²+2х-35=0
Д=2²-4*(-35)=144=12²
х₁=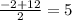 х₂=
х₂=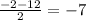
***
квадратное уравнение — это уравнение вида ax² + bx + c = 0,
где
a — первый коэффициент, не равный нулю
b — второй коэффициент
c — свободный член.
решаем с дискриминанта:
1) x² - x - 90 = 0
a = 1, b = -1, c = -90
D = b² - 4ac = (-1)² - 4 · 1 · (-90) = 361 >0
т.к. дискриминант больше нуля, то квадратное уравнение имеет два различных действительных корня
=>
X₁ = (-b+√D) / 2a = ( -(-1) + √361 ) / 2 · 1 = 1 + 19 / 2 = 20/2 = 10
X₂ = (-b-√D) / 2a = ( -(-1) - √361 ) / 2 · 1 = 1 - 19 / 2 = -18/2 = -9
2) x² + 6x + 9 = 0
a = 1, b = 6, c = 9
D = b² - 4ac = (6)² - 4 · 1 · 9 = 36 - 36 = 0
т.к. дискриминант равен нулю, то квадратное уравнение имеет только один действительный корень
=>
X₁,₂ = (-b±√D) / 2a = ( (-6) ±√D ) / 2
3) 5x² + 4x + 7 = 0
a = 5, b = 4, c = 7
D = b² - 4ac = (4)² - 4 · 5 · 7 = 16 - 140 = - 124 < 0
т.к. дискриминант меньше нуля, значит не существует вещественных корней, а только комплексные корни
4) x² + 2x - 35 = 0
a = 1, b = 2, c = -35
D = b² - 4ac = (2)² - 4 · 1 · (-35) = 4 - (-140) = 4 + 140 = 144
т.к. дискриминант больше нуля, то квадратное уравнение имеет два различных действительных корня
=>
X₁ = (-b+√D) / 2a = ( (-2) + √144 ) / 2 · 1 = (-2 + 12) / 2 = 10/2 = 5
X₂ = (-b-√D) / 2a = ( (-2) - √144 ) / 2 · 1 = (-2 - 12) / 2 = -14/2 = -7