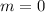Пусть х км/ч - это скорость, с которой ехал велосипедист из пункта А в пункт В Так как длина путь из пункта А в пункт В = 27 километров. Тогда путь из пункста А в пункт В он проехал за 27/х(часов) - потому что на обратном пути велосипедист уменьшил скорость на 3км/ч, следовательно: х-3км/ч - скорость велосипедиста.(потому что обратный путь был короче на 7 километров), то есть он равен: 27-7=20(км), следовательно: 20/(х-3) часов - это он потратил на обратный путь. А по условию на обратный путь он затратил всего 10минут, а это 1/6 часа меньше. Составим уравнение: 27/х-1/6=20/(х-3) Надо обе части умножить на 6х*(х-3) не равное нулю, тоесть х≠0 и х≠3(ЭТО НАМ НЕ ПОДХОДИТ)=> 162*(х-3)-х*(х-3)=120х 162х-486-х2+3х-120=0 Теперь на всё это умножить на (-1) и привести конечно-же подобные слогаемые. х2-45х+486=0 Всё получим мы через теорему Виета: х1+х2=45 х1*х2=486 х1=18 х2=27 Либо через Дискриминант, то будет так. Дискриминант=(-45)2-4*2*486=2025+1944=3969 х1,2=54(плюс/минус)63/4 х1 = 18 х2 = 27 Здесь мы видим, что оба корня нам подходят. Итак велосипедист ехал со скоростью 18 км/ч или со скоростью 27 км/ч из пункта А в пункт В. ответ: 18км/ч, 27км/ч.
Это уравнение всегда является квадратным относительно переменной х, а значит, максимум может быть два корня. Здесь это и требуется.
Ситуация, когда один корень равен другому, даже если этот корень 0, не подходит. На это есть ограничение D>0
По теореме Виета мы должны получить, что сумма корней равна 0, а их произведение всегда меньше 0.
Тогда получается, что
из этой системки (из 1-го уравнения) получаем, что m=0 или m=4, но из второго условия (неравенства) явно получаем, что m<1 и поэтому m=4 не годится. Осталось лишь ограничение D>0. Можно, конечно, было бы сказать, что при одном корне знак произведения всегда неотрицателен, а когда 0 корней, то вообще говорить не о чем. Пути 2: либо проверить само значение m=0, либо проверить D>0, например, если бы таких значений было бесконечно много.
Почему вообще это надо делать: теорема Виета работает прекрасно в любом квадратном уравнении. И вообще у уравнения n-ой степени (ограничимся здесь лишь обычными многочленами) всегда n корней по следствию из основной теоремы алгебры, правда, корни эти комплексные (множество действительных чисел является подмножеством комплексных чисел), так что у квадратного уравнения, на самом деле, всегда 2 корня, но не забивайте себе этим голову, просто примите к сведению, что D>0 здесь тоже надо бы проверить (а проще гораздо проверить само m=0)
Для того чтобы найти, на каких промежутках D>0, надо решить уравнение сначала D=0. Но там 4 страшных корня, 2 из которых действительные и нужны нам. Так что, как показывает практика, в эти дебри лучше не лезть. Но ради интереса я прикреплю картинки с формулами этих чисел. При подстановке m=0 D=12>0, что подходит.
И ещё раз повторю, что некоторые сведения были даны, чтобы понять, что в математике все не просто так и иногда какие-то вещи на самом деле гораздо более глубокие, чем мы думаем.
Итак, есть уравнение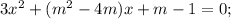
Это уравнение всегда является квадратным относительно переменной х, а значит, максимум может быть два корня. Здесь это и требуется.
Ситуация, когда один корень равен другому, даже если этот корень 0, не подходит. На это есть ограничение D>0
По теореме Виета мы должны получить, что сумма корней равна 0, а их произведение всегда меньше 0.
Тогда получается, что
из этой системки (из 1-го уравнения) получаем, что m=0 или m=4, но из второго условия (неравенства) явно получаем, что m<1 и поэтому m=4 не годится. Осталось лишь ограничение D>0. Можно, конечно, было бы сказать, что при одном корне знак произведения всегда неотрицателен, а когда 0 корней, то вообще говорить не о чем. Пути 2: либо проверить само значение m=0, либо проверить D>0, например, если бы таких значений было бесконечно много.
Почему вообще это надо делать: теорема Виета работает прекрасно в любом квадратном уравнении. И вообще у уравнения n-ой степени (ограничимся здесь лишь обычными многочленами) всегда n корней по следствию из основной теоремы алгебры, правда, корни эти комплексные (множество действительных чисел является подмножеством комплексных чисел), так что у квадратного уравнения, на самом деле, всегда 2 корня, но не забивайте себе этим голову, просто примите к сведению, что D>0 здесь тоже надо бы проверить (а проще гораздо проверить само m=0)
Для того чтобы найти, на каких промежутках D>0, надо решить уравнение сначала D=0. Но там 4 страшных корня, 2 из которых действительные и нужны нам. Так что, как показывает практика, в эти дебри лучше не лезть. Но ради интереса я прикреплю картинки с формулами этих чисел. При подстановке m=0 D=12>0, что подходит.
И ещё раз повторю, что некоторые сведения были даны, чтобы понять, что в математике все не просто так и иногда какие-то вещи на самом деле гораздо более глубокие, чем мы думаем.
ответ: