1) Функция определена повсюду кроме точки, в которой знаменатель превращается в ноль, x = 0.
Область определения состоит из двух интервалов D(y):(-∞;0) U (0; +∞).
В данном случае имеем одну точку разрыва x=0.
Вычислим границы слева и справа от этой точки
lim┬(x→-0)〖 (x^2-4)/x=-∞.〗
lim┬(x→+0)〖 (x^2-4)/x=+∞.〗
Итак, x=0 – точка разрыва второго рода.
Проверяем функцию на четность.
Проверим функцию - четна или нечетна с соотношений f(-x)=f(x) и f(-x)=-f(x). Итак, проверяем:
f(-x)=(〖(-x)〗^2-4)/((-x))=-(x^2-4)/x≠f(x)=-f(x).
Итак, функция нечетная, непериодическая.
2) Так как функция не имеет значения при х = 0, то график функции не пересекает ось Оу.
Приравняем функцию к нулю:
(x^2-4)/x=0.
Если переменная не равна 0, то к нулю можно приравнять только числитель:
x^2-4=0,
x^2=4,
x_1=√4=2,x_2= -2. Это точки пересечения с осью координат Ох.
Промежутки, на которых функция больше нуля: (-2; 0) и (2; +∞).
Промежутки, на которых функция меньше нуля: (-∞;-2) и (0; 2).
3) Асимптоты.
Вертикальной асимптотой является ось Оу, определённая в пункте 1).
Горизонтальные асимптоты графика функции:
Горизонтальную асимптоту найдем с предела данной функции при x->+∞ и x->-∞. Соотвествующие пределы находим:
lim┬(x→∞)〖 (x^2-4)/x=x-4/x=∞〗, значит, горизонтальной асимптоты справа не существует.
Аналогично, при x->-∞ f(x) = -∞, значит, горизонтальной асимптоты слева не существует
Наклонные асимптоты графика функции.
Уравнение наклонной асимптоты имеет вид y=kx+b. Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при lim┬( x→±∞)〖(kx+b-f(x)).〗
4) Для отыскания интервалов монотонности вычисляем первую производную функции:
〖y^'=〗〖 (2x*x-1*(x^2-4))/x^2 =(x^2+4)/x^2 .〗
Приравниваем её к нулю, (для дроби достаточно числитель):
x^2+4=0,x^2=-4.
Это уравнение не имеет решения, поэтому производная не может быть равна нулю, то есть заданная функция не имеет экстремумов.
Так как производная при любом значении переменной положительна, то функция на всей области определения возрастает.
5) Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y'' = 0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции:
y''((x2-4)/(x)) = -8/(x3) = 0
Данная функция не может быть равна нулю, поэтому перегибов у функции нет.
Интервалы выпуклости и вогнутости.
Ось Оу делит график функции на 2 интервала: (-∞; 0) и (0; +∞).
Интервалы, где функция выпуклая или вогнутая, находим по знаку второй производной : где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.
x = -1 0 1
y'' = 8 - -8
Вогнутая на промежутках: (0; ∞),
Выпуклая на промежутках: (-∞;0) .
6) На основе проведенного анализа выполняем построение графика функции. Для этого сначала строим вертикальные и наклонные асимптоты, затем находим значение функции в нескольких точках и по них проводим построение.
Первое, что я бы сделал, это избавился от дробных коэффициентов, для этого надо каждый член трёхчлена домножить на 8 и приравнять само выражение 0:
- -6x +40=0
Находим дискриминант D: 36+160=196.
= 14
Так как D > 0, значит у нас будет два x:
x1= = = 4
x2= = =-10
Квадратное уравнение разлагается на множители по формуле: a*(x-x1)(x-x2) - обратите внимание, если х1 и х2 это числовые значения, то X так и записывается X. Таким образом данное уравнение разлагается следующим образом:
ответ: -(x-4)*(x+10)
5) Действуем аналогично, только на этот раз домножаем на 4, чтобы избавится от всех дробей и получаем выражение: 2 - y -1.
Приравниваем к 0 и решаем квадратное уравнение:
D=1+8=9
D>0, значит есть x1 и x2:
x1,2= = = 1 ; -0.5.
Таким образом после разложения на множители получаем:
Дана функция у = (x^2-4)/x
1) Функция определена повсюду кроме точки, в которой знаменатель превращается в ноль, x = 0.
Область определения состоит из двух интервалов D(y):(-∞;0) U (0; +∞).
В данном случае имеем одну точку разрыва x=0.
Вычислим границы слева и справа от этой точки
lim┬(x→-0)〖 (x^2-4)/x=-∞.〗
lim┬(x→+0)〖 (x^2-4)/x=+∞.〗
Итак, x=0 – точка разрыва второго рода.
Проверяем функцию на четность.
Проверим функцию - четна или нечетна с соотношений f(-x)=f(x) и f(-x)=-f(x). Итак, проверяем:
f(-x)=(〖(-x)〗^2-4)/((-x))=-(x^2-4)/x≠f(x)=-f(x).
Итак, функция нечетная, непериодическая.
2) Так как функция не имеет значения при х = 0, то график функции не пересекает ось Оу.
Приравняем функцию к нулю:
(x^2-4)/x=0.
Если переменная не равна 0, то к нулю можно приравнять только числитель:
x^2-4=0,
x^2=4,
x_1=√4=2,x_2= -2. Это точки пересечения с осью координат Ох.
Промежутки, на которых функция больше нуля: (-2; 0) и (2; +∞).
Промежутки, на которых функция меньше нуля: (-∞;-2) и (0; 2).
3) Асимптоты.
Вертикальной асимптотой является ось Оу, определённая в пункте 1).
Горизонтальные асимптоты графика функции:
Горизонтальную асимптоту найдем с предела данной функции при x->+∞ и x->-∞. Соотвествующие пределы находим:
lim┬(x→∞)〖 (x^2-4)/x=x-4/x=∞〗, значит, горизонтальной асимптоты справа не существует.
Аналогично, при x->-∞ f(x) = -∞, значит, горизонтальной асимптоты слева не существует
Наклонные асимптоты графика функции.
Уравнение наклонной асимптоты имеет вид y=kx+b. Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при lim┬( x→±∞)〖(kx+b-f(x)).〗
Находим коэффициент k: k=lim┬(x→±∞)〖(f(x))/x.〗
k=lim┬( x→±∞)〖 (x^2-4)/x^2 =1-4/x^2 =1.〗
Коэффициент b: b=〖lim┬(x→±∞) (〗〖f(x)-kx).〗
〖b=lim〗┬( x→±∞)〖 (x^2-4)/x-x=(x^2-4-x^2)/x=-4/x=0.〗
Конечный вид асимптоты следующий: y=x.
4) Для отыскания интервалов монотонности вычисляем первую производную функции:
〖y^'=〗〖 (2x*x-1*(x^2-4))/x^2 =(x^2+4)/x^2 .〗
Приравниваем её к нулю, (для дроби достаточно числитель):
x^2+4=0,x^2=-4.
Это уравнение не имеет решения, поэтому производная не может быть равна нулю, то есть заданная функция не имеет экстремумов.
Так как производная при любом значении переменной положительна, то функция на всей области определения возрастает.
5) Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y'' = 0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции:
y''((x2-4)/(x)) = -8/(x3) = 0
Данная функция не может быть равна нулю, поэтому перегибов у функции нет.
Интервалы выпуклости и вогнутости.
Ось Оу делит график функции на 2 интервала: (-∞; 0) и (0; +∞).
Интервалы, где функция выпуклая или вогнутая, находим по знаку второй производной : где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.
x = -1 0 1
y'' = 8 - -8
Вогнутая на промежутках: (0; ∞),
Выпуклая на промежутках: (-∞;0) .
6) На основе проведенного анализа выполняем построение графика функции. Для этого сначала строим вертикальные и наклонные асимптоты, затем находим значение функции в нескольких точках и по них проводим построение.
Таблица точек
x y
-4.0 -3
-3.5 -2.4
-3.0 -1.7
-2.5 -0.9
-2.0 0
-1.5 1.2
-1.0 3
-0.5 7.5
0 -
0.5 -7.5
1.0 -3
1.5 -1.2
2.0 0
2.5 0.9
3.0 1.7
3.5 2.4
4.0 3 .
4) -(x-4)*(x+10)
5) 2(x-1)(x+0.5)
Объяснение:
4)
Первое, что я бы сделал, это избавился от дробных коэффициентов, для этого надо каждый член трёхчлена домножить на 8 и приравнять само выражение 0:
-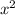 -6x +40=0
-6x +40=0
Находим дискриминант D: 36+160=196.
Так как D > 0, значит у нас будет два x:
x1=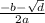 =
= 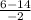 = 4
= 4
x2=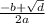 =
= 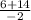 =-10
=-10
Квадратное уравнение разлагается на множители по формуле: a*(x-x1)(x-x2) - обратите внимание, если х1 и х2 это числовые значения, то X так и записывается X. Таким образом данное уравнение разлагается следующим образом:
ответ: -(x-4)*(x+10)
5) Действуем аналогично, только на этот раз домножаем на 4, чтобы избавится от всех дробей и получаем выражение: 2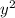 - y -1.
- y -1.
Приравниваем к 0 и решаем квадратное уравнение:
D=1+8=9
D>0, значит есть x1 и x2:
x1,2=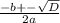 =
= 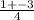 = 1 ; -0.5.
= 1 ; -0.5.
Таким образом после разложения на множители получаем:
ответ: 2(x-1)(x+0.5).