Рассмотри все последовательности из нулей и единиц длины 10. Что из перечисленного является соответствием между множествами последовательностей с чётным и нечётным числом единиц? 1) Каждой последовательности с чётным числом единиц сопоставляется последовательность, в которой первый символ заменён на противоположный (например, 0000→1000)
2) Каждой последовательности с чётным числом единиц сопоставляется последовательность, в которой последний символ заменён на противоположный (например, 0000→0001)
3) Каждой последовательности с чётным числом единиц сопоставляется последовательность, в которой каждый символ заменён на противоположный (например, 1001→0110)
4) Каждой последовательности с чётным числом единиц сопоставляется последовательность, в которой каждая цифра, кроме первой, заменена на противоположную (например, 1001→1110)
5) Каждой последовательности с чётным числом единиц сопоставляется последовательность, в которой k-ая цифра равна остатку от деления на 2 суммы первых k цифр (например, 1001→1110)

1) х вершины = -b / 2a; х = 2 / -2 = -1.

у вершины = -1 + 2 + 3 = 4.

--------------------------------------

Хв = -1

Ув = 4

2) Ось симметрии параболы проходит через вершину. С этого график оси симметрии: x = -1.

--------------------------------------

х = -1

3) Точки пересечения с осью Х - корни квадратного уравнения. С этого они ровни:

-x^2 - 2x + 3 = 0,

x^2 + 2x - 3 = 0.

За теоремой Виета: x1 = -3; x2 = 1.

Точки пересечения с осью У узнаю подставляя вместо х 0.

0 - 0 + 3 = 3.

--------------------------------------

( 0, 3 ), ( -3, 0 ), ( 1, 0 )

4) График в фото

5) -x^2 - 2x + 3 > 0;

Используя график видим, что функция больше 0 при х є ( -3 ; 1 ).

--------------------------------------

х є ( -3 ; 1 )

Сначала построим график функции, которая под модулем. Что делает модуль? Он все отрицательные ЗНАЧЕНИЯ делает положительными, то есть получив график функции нам надо будет всё что ниже оси Ох поднять наверх (отразить относительно оси Ох).

И так надо построить этот график. Это парабола, ветви которой вверх, координаты вершины (1/3;-4/3). И найдём точки пересечения с осями координат: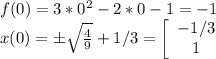

Можем строить.

И так надо отразить относительно оси Ох значения функции f(x) на интервале от -1/3 до 1. Получилась нужная нам функция, её можно записать как:

И естественно так как мы отразили относительно оси Ох, то значения вершины и точка пересечения с осью Оу.