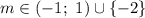Расстояние между двумя пристанями равно 148 км. Из них одновременно навстречу друг другу вышли две лодки, скорости которых в стоячей воде равны. Через 2 ч. лодки встретились. Скорость течения реки равна 2 км/ч.
Скорость лодки в стоячей воде равна
км/ч.
Сколько километров до места встречи пройдёт лодка, плывущая по течению?
км.
Сколько километров до места встречи пройдёт лодка, плывущая против течения?
км.
Объяснение:
1)(2a - 5b)·(... - ...) = 6a^3 - 15a^2*b - 14ab + ...;
6a^3 : 2a = 3a^2
14ab : 2a = 7b
(2a - 5b)(3a^2 - 7b) = 6a^3 - 15a^2*b - 14ab + 35b^2
2)(... - ...)·(6x^2 - 5y^2) = 12x^3 + 42x^2*y - ... - 35y^3;
12x^3 : 6x^2 = 2x
-35y^3 : (-5y^2) = 7y
(2x + 7y)(6x^2 - 5y^2) = 12x^3 + 42x^2*y - 10xy^2 - 35y^3
3)(3a + 4c)·(... + ...) = 20ac + 8bc + 6ab + ...;
20ac : 4c = 5a
6ab : 3a = 2b
(3a + 4c)(5a + 2b) = 20ac + 8bc + 6ab + 15a^2
4)(... + ...)·(2a + 5b) = ... + 5ab + 8ac + 20b
Здесь опечатка, в конце должно быть 20bc
5ab : 5b = a
8ac : 2a = 4c
(a + 4c)(2a + 5b) = 2a^2 + 5ab + 8ac + 20bc
Найдём вершину параболы:
В данной точке можно обозначить опорную прямую, которая будет симметрична для ветвей (тогда значения с одной стороны можно просто симметрично перенести на другую)
Возьмём 3 точки (при ограничении прямой x < 3 даже 3-ёх много будет)
1) x = 5
2) x = 6
3) x = 7
Отмечаем точки на координатной плоскости и симметрично их копируем относительно вс прямой
Не стоит забывать что условие ограничения функции x ≥ 3, поэтому переносим только точку, симметричную B; позже на графике эта точка будет закрашена и обозначена как A
(картинка 1)
Разбираемся со вторым графиком
Уравнение прямой, достаточно двух точек
Условие x < 3, точка (3; 1) выколота
(картинка 2)
y = m
При m = 1 (и всё что выше) получаем 1 точку пересечения
Следовательно, подходят все значения до m = 1
При m = -1 и до m = -2 имеем 3 точки пересечения
При m = -2 2 точки пересечения (вершина параболы и прямая)
Следовательно нам подходят значения -2; от -1 до 1 не включительно
ответ: