Расстояние от лагеря до села 15 км из лагеря до села вышли одновременно два туриста скорость 1 туриста на 2 км/ч больше второго туриста и поэтому 1 турист пришел на 1ч 15 мин раньше 2 туриста какова скорость 1 туриста
1. Смотри, в первом примере тебе нужно раскрыть скобки. Т.е. ты -4x^3 умножаешь на каждый член стоящий в скобках. При этом не забывай,что -4x^3-отрицательное, т.е. перед ним стоит знак минус. Если наоборот перед числом не стоит знак минус , значит оно положительное.
Следует помнить,что при перемножении членов их ЗНАКИ также перемножаются. При умножении минуса на плюс получаем минус. При умножении минуса на минус получаем плюс.
Еще необходимо отметить, что при перемножении членов с одинаковыми основаниями(Например икс умножить на икс или игрек умножить на игрек и т.д) показатели их степеней складываются.
В итоге получаем:
2. Во втором примере похожая ситуация. Только тебе нужно уже раскрыть две скобки. чтобы этого добиться, необходимо каждый член первой скобки умножить на каждый член второй скобки. Т.е. тебе 1 из первой скобки нужно умножить на 2у и потом на х, а -2х тебе нужно умножить на 2у и потом на х.
В итоге получаем:
3. Третий пример совсем легкий. Дело в том, что это квадрат разности. Квадрат разности раскрывается по следующему закону:
Это такое правило,которому нужно следовать. Т.е. тебе нужно повторить тоже самое, только используя свои слагаемые.
Поскольку выражение под корнем должно быть неотрицательным, область определения - те иксы, при которых
Если это неравенство выполняется при всех , то областью определения функции будет любое число.
Графиком функции в левой части является парабола, ветви которой направлены вверх. Парабола может пересечь ось не более чем в двух точках. Чтобы неравенство было верным для всех необходимо, чтобы эта парабола имела не более 1 точки пересечения с осью - т.е. либо одну, либо их вообще не должно быть. Ровно одна точка пересечения будет только в том случае, если уравнения имеет одно решение (это возможно при ). Точек пересечения не будет вообще только в том случае, если уравнение не имеет решений (это возможно при ). Оба условия нужно объединить: неравенство будет выполнено всегда, если .
Тут все очень просто.
1. Смотри, в первом примере тебе нужно раскрыть скобки. Т.е. ты -4x^3 умножаешь на каждый член стоящий в скобках. При этом не забывай,что -4x^3-отрицательное, т.е. перед ним стоит знак минус. Если наоборот перед числом не стоит знак минус , значит оно положительное.
Следует помнить,что при перемножении членов их ЗНАКИ также перемножаются. При умножении минуса на плюс получаем минус. При умножении минуса на минус получаем плюс.
Еще необходимо отметить, что при перемножении членов с одинаковыми основаниями(Например икс умножить на икс или игрек умножить на игрек и т.д) показатели их степеней складываются.
В итоге получаем:
2. Во втором примере похожая ситуация. Только тебе нужно уже раскрыть две скобки. чтобы этого добиться, необходимо каждый член первой скобки умножить на каждый член второй скобки. Т.е. тебе 1 из первой скобки нужно умножить на 2у и потом на х, а -2х тебе нужно умножить на 2у и потом на х.
В итоге получаем:
3. Третий пример совсем легкий. Дело в том, что это квадрат разности. Квадрат разности раскрывается по следующему закону: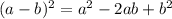
Это такое правило,которому нужно следовать. Т.е. тебе нужно повторить тоже самое, только используя свои слагаемые.
В итоге у тебя должно получиться следующее:
ну вот и все. Как видишь, все довольно просто.
Удачи в покорении математических вершин:)
Поскольку выражение под корнем должно быть неотрицательным, область определения - те иксы, при которых
Если это неравенство выполняется при всех
, то областью определения функции будет любое число.
Графиком функции в левой части является парабола, ветви которой направлены вверх. Парабола может пересечь ось
не более чем в двух точках. Чтобы неравенство было верным для всех 
необходимо, чтобы эта парабола имела не более 1 точки пересечения с осью 
- т.е. либо одну, либо их вообще не должно быть. Ровно одна точка пересечения будет только в том случае, если уравнения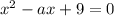 
имеет одно решение (это возможно при 
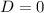). Точек пересечения не будет вообще только в том случае, если уравнение 
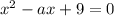не имеет решений (это возможно при 
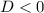). Оба условия нужно объединить: неравенство будет выполнено всегда, если 
.
Ищем дискриминант:
ОТВЕТ: при![a\in[-6;6]](/tpl/images/1334/6693/49fa6.png)