Разложи на множители: (y6+x6)2−(y6−x6)2−y2x2. (Может быть несколько вариантов ответа! Выбери все возможные варианты, которые могут получиться.)

x2(4y6x4+2x10−y2x)
4y6x6+2x12−y2x2
(2y3x3−yx)⋅(2y3x3+yx)
Другой ответ
x2(2x4−y2x)
y2x2⋅(4y4x4−1)
y2x2⋅(2y2x2−1)⋅(2y2x2+1)

Показать ответ

Ответ:

ALBERTALBERT2004

23.11.2022 00:21

ответ: x = ±√3

Объяснение:

можно двумя решить (выбирайте-какой больше понравится...)

1) 3 = (√3)²

3*(х+2)² = (√3)² * (х+2)² = ( √3(х+2) )²

получили выражение вида: a² = b² --> |a| = |b| --> a = ±b

или 2х + 3 = √3*х + 2√3 --> 2x - √3*x = 2√3 - 3 --> x(2-√3) = √3(2-√3)

x = √3

или 2х + 3 = -√3*х - 2√3 --> 2x + √3*x = -2√3 - 3 --> x(2+√3) = -√3(2+√3)

x = -√3

2) т.к. х=-2 НЕ является решением уравнения (корнем) - это можно проверить устно: (-4+3)² ≠ 3*0²,

то обе части равенства можно разделить на (x+2)² ≠ 0

получим: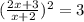 $(\frac{2x+3}{x+2}) ^{2} =3$

$\frac{2x+3}{x+2} =\sqrt{3}$ или $\frac{2x+3}{x+2} =-\sqrt{3}$

продолжение решения аналогично 1)

или можно выделить целую часть:

$\frac{2x+4-1}{x+2} =\sqrt{3}$ --> $\frac{2x+4}{x+2} -\frac{1}{x+2} =\sqrt{3}$ --> $2-\frac{1}{x+2} =\sqrt{3}$ --> $\frac{1}{x+2} =2-\sqrt{3}$

$x+2=\frac{1}{2-\sqrt{3} }$

$x+2=\frac{2+\sqrt{3} }{(2-\sqrt{3})(2+\sqrt{3} ) }$

$x+2=2+\sqrt{3}$ --> x = √3 ( второе ("с минусом" -√3) аналогично)

0,0(0 оценок)

Ответ:

mariana20021

25.02.2023 11:49

Решить систему уравнений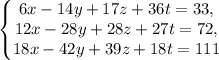 $\left\{\begin{matrix}6x-14y+17z+36t=33, \\ 12x-28y+28z+27t=72, \\ 18x-42y+39z+18t=111\end{matrix}\right.$ и выделить общее решение соответствующей однородной системы и частное решение неоднородной.

Решение. Выпишем расширенную матрицу системы и будем выполнять элементарные преобразования строк данной матрицы.

$\overline{A} =\begin{pmatrix}\begin{matrix}6 \\ 12 \\ 18 \end{matrix} \ \ \begin{matrix}-14 \\ -28 \\ -42 \end{matrix} \ \ \begin{matrix}17 \\ 28 \\ 39 \end{matrix} \ \ \begin{matrix}36 \\ 27 \\ 18 \end{matrix} \ \begin{matrix}| \\ | \\ |\end{matrix} \ \begin{matrix}33 \\ 72 \\ 111 \end{matrix}\end{pmatrix} \sim$ $\begin{pmatrix}\begin{matrix}6 \\ 0 \\ 0 \end{matrix} \ \ \begin{matrix}-14 \\ 0 \\ 0 \end{matrix} \ \ \begin{matrix}17 \\ -6 \\ -12 \end{matrix} \ \ \begin{matrix}36 \\ -45 \\ -90 \end{matrix} \ \begin{matrix}| \\ | \\ |\end{matrix} \ \begin{matrix}33 \\ 6 \\ 12 \end{matrix}\end{pmatrix} \sim$ $\begin{pmatrix}\begin{matrix}6 \\ 0 \\ 0 \end{matrix} \ \ \begin{matrix}-14 \\ 0 \\ 0 \end{matrix} \ \ \begin{matrix}17 \\ 6 \\ 0 \end{matrix} \ \ \begin{matrix}36 \\ 45 \\ 0 \end{matrix} \ \begin{matrix}| \\ | \\ |\end{matrix} \ \begin{matrix}33 \\ -6 \\ 0 \end{matrix}\end{pmatrix}.$

Вычислим ранг данной матрицы: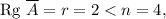 $\text{Rg} \ \overline{A} = r = 2 < n = 4,$ где 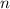- число неизвестных. Система имеет нетривиальные решения. Базисный минор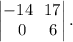 $\begin{vmatrix}-14 \ \ 17 \\ \ \ 0 \ \ \ \ 6\end{vmatrix}.$

Ставим в соответствие расширенной матрице упрощенную систему:

$\left \{ {\bigg{6x - 14y + 17z + 36t = 33,} \atop \bigg{6z + 45t = -6, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }} \right.$

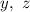где $y, \ z$ - базисные переменные, 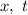$x, \ t$ - свободные переменные.

Положив значения свободных переменных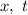 $x, \ t$ равными нулю, получим частное решение неоднородной системы: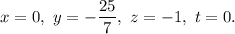 $x=0, \ y = -\dfrac{25}{7}, \ z = -1, \ t = 0.$

$\left \{ {\bigg{6x - 14y = 33-36t-17z,} \atop \bigg{z = \dfrac{-6-45t}{6}; \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }} \right.$

$\left \{ {\bigg{6x - 14y = 33-36t-17(-1-7,5t) =50+91,5t,} \atop \bigg{z = -1-7,5t; \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }} \right.$

$\left \{ {\bigg{y=\dfrac{6x-50-91,5t}{14}, } \atop \bigg{z=-1-7,5t. \ \ \ \ \ \ \ \ }} \right.$

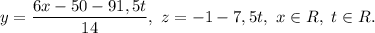
Общее решение: $y = \dfrac{6x-50-91,5t}{14}, \ z = -1-7,5t, \ x \in R, \ t \in R.$

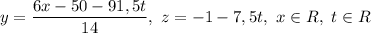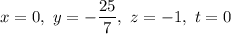ответ: $y = \dfrac{6x-50-91,5t}{14}, \ z = -1-7,5t, \ x \in R, \ t \in R$ - общее решение; $x=0, \ y = -\dfrac{25}{7}, \ z = -1, \ t = 0$ - частное решение.