Разложите числа в произведения степеней простых чисел : 70, 240, 168

Показать ответ

Ответ:

rusrusik

27.04.2022 00:59

Пример

Последовательность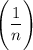 $\Bigg(\dfrac{1}{n}\Bigg)$ монотонно стремится к нулю, поэтому по признаку Лейбница ряд сходится. Найдем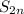 $S_{2n}$

$S_{2n}=1-\dfrac{1}{2}+\dfrac{1}{3}-...+\dfrac{1}{2n-1}-\dfrac{1}{2n}=\\ \\ =1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2n}-\Bigg(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{n}\Bigg)~~\boxed{=}$

Выпишу формулу Эйлера)))) Пусть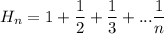 $H_n=1+\dfrac{1}{2}+\dfrac{1}{3}+...\dfrac{1}{n}$ . Эйлер получил асимптотическое выражение для суммы первых n членов ряда:

$H_n=\ln n+C+\varepsilon_n$

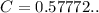где C=0.57772.. - постоянная Эйлера, при 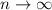$n\to \infty$ значение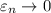 $\varepsilon_n\to0$

$\boxed{=}~~C+\ln 2n+\varepsilon_{2n}-\Big(C+\ln n+\varepsilon_n\Big)=\ln 2+\varepsilon_{2n}-\varepsilon_{n}$

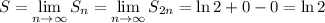
Следовательно, $\displaystyle S=\lim_{n \to \infty} S_n= \lim_{n \to \infty} S_{2n}=\ln 2+0-0=\ln2$

(S_n) - последовательность частичных сумм данного ряда.

Это мы показали что тот ряд равен ln 2. Теперь перейдем к нашем заданию.

$1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{2a-1}-\dfrac{1}{2}-\dfrac{1}{4}-...-\dfrac{1}{2b}+\dfrac{1}{2a+1}+\dfrac{1}{2a+3}+\\ \\ \\ +...+\dfrac{1}{4b-1}-...$

В силу примера, что мы показали в начале, мы получим

$1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{2a-1}-\bigg(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2b}\bigg)+\\ \\ \\ +\bigg(\dfrac{1}{2a+1}+\dfrac{1}{2a+3}+...+\dfrac{1}{4b-1}\bigg)-...$

Первые две скобки - ряда сходятся, теперь нужно показать что последнее тоже сходится. Рассмотрим ряд

$\displaystyle \sum^{\infty}_{n=1}\bigg(\dfrac{1}{2(n-1)a+1}+\dfrac{1}{2(n-1)a+3}+...+\dfrac{1}{2na-1}-\\ \\ \\ -\dfrac{1}{2(n-1)b+2}-\dfrac{1}{2(n-1)b+4}-...-\dfrac{1}{2nb}\bigg)$

Пусть a > b, тогда

$S_n=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2nb}+\dfrac{1}{2nb+1}+\dfrac{1}{2nb+3}+...+\dfrac{1}{2nb-3}$

Тут (Sn) - последовательность частичных сумм исследуемого ряда.

Прибавляя и вычитая в выражение слагаемое, мы получим

$S_n=\dfrac{1}{2nb+2}+\dfrac{1}{2nb+4}+...+\dfrac{1}{2na}=\dfrac{1}{2}\bigg(\dfrac{1}{nb+1}+\dfrac{1}{nb+2}+...+\dfrac{1}{na}\bigg)$

По формуле Эйлера

$S_n=C_{2na}+\ln\dfrac{2na}{2nb}-\dfrac{1}{2}\ln\dfrac{na}{nb}+\delta_n$

Переходя к пределу при n стремящихся к бесконечности, мы получим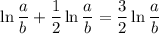 $\ln \dfrac{a}{b}+\dfrac{1}{2}\ln \dfrac{a}{b}=\dfrac{3}{2}\ln \dfrac{a}{b}$

Для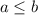 $a\leq b$ аналогичным образом получается тот же результат. В частности если a = 2, b = 1, получим

$1+\dfrac{1}{3}-\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{4}+...\dfrac{3}{2}\ln\dfrac{2}{1}=\dfrac{3}{2}\ln2$

0,0(0 оценок)

Ответ:

scream75821

03.05.2023 13:48

Пусть v1 км/ч и v2 км/ч - скорости первого и второго велосипедистов соответственно. За время t=15 мин=1/4 ч. первый велосипедист продет расстояние s1=v1*t=v1/4 км, а второй велосипедист - расстояние s2=v2*t=v2/4 км. По условию, v1/4=v2/4+2, откуда v1=v2+8 км/ч. Пусть R - радиус окружности, по которой едет второй велосипедист, тогда 4*R - радиус окружности, по которой едет первый велосипедист. Пусть n - число оборотов, которое совершит за 15 мин. первый велосипедист, тогда s1=2*π*4*R*n=8*π*R*n км. Тогда за это время второй велосипедист совершит 3*n оборотов, поэтому s2=2*π*R*3*n=6*π*R*n км. Составим пропорцию:

s1/s2=v1*t/(v2*t)=8*π*R*n/(6*π*R*n), откуда v1/v2=8/6=4/3 и v1=4/3*v2. Таким образом, получена система уравнений:

v1=v2+8

v1=4/3*v2

Решая её, находим v2=24 км/ч и v1=32 км/ч.

ответ: 32 и 24 км/ч.

0,0(0 оценок)

Популярные вопросы: Алгебра