Характеристическое уравнение r²-8r+16=0; r1=r2=4. Общее решение однородного уравнения: Y=(C1 +C2•х) •e^4x Общее решение – y=Y+Y1, где Y1 - частное решение заданного уравнения, которое ищется в виде Y1=ax²•e^4x. => Y1’= 2ax•e^4x+4ax²•e^4x=2e^4x•(ax+2ax²); Y1”=8e^4x•(ax+2ax²)+2e^4x•(a+4ax)= e^4x•(16ax²+8ax+8ax+2a) Тогда 16ax²+16ax+2a-16ax-32ax²+16 ax²=1 2a=1 =:> a=1/2 или Y1=(x²•e^4x)/2
Тогда общее решение заданного уравнения: у=(C1 +C2•х) •e^4x+(x²•e^4x)/2=(e^4x)•( C1 +C2•х+x²/2) Находим У’ и, подставляя заданные начальные условия, находим С1 и С2 для этих условий. у'=4•(e^4x)•( C1 +C2•х+x²/2)+ (e^4x)•(C2+x) y(0)=C1=0; y’(0)=4C1+C2=1 => C2=1. Подставляя найденные значения С1 и С2 в общее решение получаем искомое частное решение заданного уравнения у= (e^4x)•(х+x²/2). пыталась как можно проще написать примерно так
Общее решение однородного уравнения: Y=(C1 +C2•х) •e^4x
Общее решение – y=Y+Y1, где Y1 - частное решение заданного уравнения, которое ищется в виде Y1=ax²•e^4x. => Y1’= 2ax•e^4x+4ax²•e^4x=2e^4x•(ax+2ax²);
Y1”=8e^4x•(ax+2ax²)+2e^4x•(a+4ax)= e^4x•(16ax²+8ax+8ax+2a)
Тогда
16ax²+16ax+2a-16ax-32ax²+16 ax²=1
2a=1 =:> a=1/2 или Y1=(x²•e^4x)/2
Тогда общее решение заданного уравнения:
у=(C1 +C2•х) •e^4x+(x²•e^4x)/2=(e^4x)•( C1 +C2•х+x²/2)
Находим У’ и, подставляя заданные начальные условия, находим С1 и С2 для этих условий.
у'=4•(e^4x)•( C1 +C2•х+x²/2)+ (e^4x)•(C2+x)
y(0)=C1=0;
y’(0)=4C1+C2=1 => C2=1.
Подставляя найденные значения С1 и С2 в общее решение получаем искомое частное решение заданного уравнения
у= (e^4x)•(х+x²/2). пыталась как можно проще написать примерно так
Могу предложить несколько корявое, но все же решение... наверное.
Обозначим за a и b цифры искомого числа. Тогда из условия задачи это число есть
приравняем выражения, будем считать a переменной величиной, а b какой-то постоянной, тогда это будет квадратным уравнением относительно a :
Решая обычным образом находим
Мы знаем, что a и b - цифры, т.е. они могут быть лишь величинами 0 1 2 3 4 5 6 7 8 9
Смотрим, при самых очевидных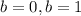
корень нормально извлекается.
Тогда
Из всех возможных двузначных чисел (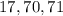
) подходящим оказывается только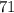 
Подтвердить это можно только непосредственной проверкой