В решении.
Объяснение:
√52 - 10√27 - √52 - 10√27;
1) Нужно разложить первое подкоренное выражение на квадрат разности.
10√27 = 2 * 5 * √27 (удвоенное произведение первого числа на второе).
Значит, первое число = 5, второе √27.
Преобразованное выражение под корнем:
√25 - 10√27 + 27 = √(5 - √27)² = |5 - √27| = √27 - 5.
Квадрат первого числа - удвоенное произведение первого числа на второе + квадрат второго числа.
Так как √27 больше 5, то |5 - √27| = -(5 - √27) = √27 - 5.
2) Разложить второе подкоренное выражение на квадрат суммы:
√25 + 10√27 + 27 = √(5 + √27)² = |5 + √27| = 5 + √27.
Квадрат первого числа + удвоенное произведение первого числа на второе + квадрат второго числа.
Так как сумма в модуле положительная, то |5 + √27| = 5 + √27.
3) Вычитание:
√27 - 5 - (5 + √27) = √27 - 5 - 5 - √27 = -10. ответ примера.
прощения, но решение получилось слишком сложным :(
q - знаменатель геом. прогр.
d - сумма арифм. прогрессии
a - первый член ар. прогр.
b - первый член геом. прогр.
1) a+d+a+2d=2a+3d=12; также b+bq=b(1+q)=12; также bq+a+d=12
2) a+2d=bq
3) a+d=b
4) a+bq^2=14
из b(1+q)=12:
из a+2d=bq и a+d=b выражаем b+d=bq -> d=bq-b=b(q-1)
т.е.
из a+bq^2=14 выразим a=14
Подставим в 2a+3d=12 получим квадратное уравнение вида:
После всех приведений и сокращений и с учетом, что занменатель д.б. не равен 0, получим:
Решая єто уравнения получим, что q=5/3 - не подходит, т.к. в условии числа д.б. целыми и q=1/2.
Отсюда b=8, a=12, d=-4
Получаем последовательность:
12 8 4 2
В решении.
Объяснение:
√52 - 10√27 - √52 - 10√27;
1) Нужно разложить первое подкоренное выражение на квадрат разности.
10√27 = 2 * 5 * √27 (удвоенное произведение первого числа на второе).
Значит, первое число = 5, второе √27.
Преобразованное выражение под корнем:
√25 - 10√27 + 27 = √(5 - √27)² = |5 - √27| = √27 - 5.
Квадрат первого числа - удвоенное произведение первого числа на второе + квадрат второго числа.
Так как √27 больше 5, то |5 - √27| = -(5 - √27) = √27 - 5.
2) Разложить второе подкоренное выражение на квадрат суммы:
10√27 = 2 * 5 * √27 (удвоенное произведение первого числа на второе).
Значит, первое число = 5, второе √27.
Преобразованное выражение под корнем:
√25 + 10√27 + 27 = √(5 + √27)² = |5 + √27| = 5 + √27.
Квадрат первого числа + удвоенное произведение первого числа на второе + квадрат второго числа.
Так как сумма в модуле положительная, то |5 + √27| = 5 + √27.
3) Вычитание:
√27 - 5 - (5 + √27) = √27 - 5 - 5 - √27 = -10. ответ примера.
прощения, но решение получилось слишком сложным :(
q - знаменатель геом. прогр.
d - сумма арифм. прогрессии
a - первый член ар. прогр.
b - первый член геом. прогр.
1) a+d+a+2d=2a+3d=12; также b+bq=b(1+q)=12; также bq+a+d=12
2) a+2d=bq
3) a+d=b
4) a+bq^2=14
из b(1+q)=12:
из a+2d=bq и a+d=b выражаем b+d=bq -> d=bq-b=b(q-1)
т.е.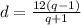
из a+bq^2=14 выразим a=14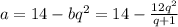
Подставим в 2a+3d=12 получим квадратное уравнение вида:
После всех приведений и сокращений и с учетом, что занменатель д.б. не равен 0, получим:
Решая єто уравнения получим, что q=5/3 - не подходит, т.к. в условии числа д.б. целыми и q=1/2.
Отсюда b=8, a=12, d=-4
Получаем последовательность:
12 8 4 2